Examples

NV center - DC Magnetometry

class Magnetometry(particle_filter: ParticleFilter, phys_model: NVCenter, control_strategy: Callable, simpars: SimulationParameters, cov_weight_matrix=None, eta_flag: bool = False, extraction_flag: bool = False, cov_flag: bool = False)

Bases: StatelessMetrology

Simulates the estimation of a magnetic field with a mean square error loss. This class is suitable for a neural network agent, for a static strategy, and for other simple controls known in the literature, like the $\sigma^{-1}$ strategy and the particle guess heuristic (PGH). It works both for static and for oscillating magnetic fields.

Constructor of the Magnetometry class.

Parameters

particle_filter: ParticleFilter

Particle filter responsible for the update of the Bayesian posterior on the parameters and on the state of the probe. It contains the methods for applying the Bayes rule and computing Bayesian estimators from the posterior.

phys_model: NVCenter

Abstract description of the parameters encoding and of the measurement on the NV center.

control_strategy: Callable

Callable object (normally a function or a lambda function) that computes the values of the controls for the next measurement from the Tensor input_strategy. This class expects a callable with the following header

controls = control_strategy(input_strategy)

It is typically a wrapper for the neural network or a vector of static controls.

simpars: SimulationParameters

Contains the flags and parameters that regulate the stopping condition of the measurement loop and modify the loss function used in the training.

cov_weight_matrix: List, optional

Weight matrix that determines the relative contribution to the total error of the parameters in phys_model.params. It is list of float representing a positive semidefinite matrix. If this parameter is not passed then the default weight matrix is the identity, i.e. $G=\text{Id}$ .

eta_flag: bool = False

This flag controls the addition of a normalization factor to the MSE loss.

If eta_flag is True, the MSE loss is divided by the normalization factor

(55) $\eta = \min \left( \sum_{i=1}^d G_{ii} \frac{(b_i-a_i)}{12}, \frac{1}{T} \right) \; ,$

where $(a_i, b_i)$ are the bounds of the i-th parameter in phys_model.params and $G_{ii}$ are the diagonal entries of cov_weight_matrix. $T$ is the total elapsed evolution time, which can be different for each estimation in the batch.

Achtung! This flag should be used only if the resource is the total estimation time.

extraction_flag: bool = False

If extraction_flag=True a couple of particles are sampled from the posterior and added to the input_strategy Tensor. This is useful to simulate the PGH control for the evolution time, according to which the k-th control should be

(56) $\tau_k = \frac{1}{||\vec{x}_1 - \vec{x}_2|| + \epsilon} \; ,$

with $\epsilon \ll 1$ , where $\vec{x}_1$ and $\vec{x}_2$ are respectively the first and the second particle extracted from the ensemble and $||\cdot||$ is the cartesian norm.

cov_flag: bool = False

If cov_flag=True a flattened version of the covariance matrix of the particle filter ensemble is added to the input_strategy Tensor. This is useful to simulate the $\sigma^{-1}$ control strategy and its variant that accounts for a finite transversal relaxation time. They prescribe respectively for the k-th control

(57) $\tau_k = \frac{1}{\left[ \text{tr} (\Sigma) \right]^{\frac{1}{2}} } \; ,$

and

(58) $\tau_k = \frac{1}{\left[ \text{tr} (\Sigma) \right]^{\frac{1}{2}} + \widehat{T_2^{-1}}} \; ,$

being $\Sigma$ the covariance matrix of the posterior computed with the compute_covariance() method.

generate_input(weights: Tensor, particles: Tensor, meas_step: Tensor, used_resources: Tensor, rangen: Generator): Generates the input_strategy Tensor of the generate_input() method. The returned Tensor is influenced by the parameters extract_flag and cov_flag of the constructor.

loss_function(weights: Tensor, particles: Tensor, true_values: Tensor, used_resources: Tensor, meas_step: Tensor): Mean square error on the parameters, as computed in loss_function(). The behavior of this method is influence by the flag eta_flag passed to the constructor of the class.

class NVCenter(batchsize: int, params: List[Parameter], prec: Literal['float64', 'float32'] = 'float64', res: Literal['meas', 'time'] = 'meas', control_phase: bool = False)

Bases: StatelessPhysicalModel

Model for the negatively charged NV center in diamond used for various quantum metrological task. A single measurement on the NV center consists in multiple Ramsey sequencies of the same controllable duration applied to the NV center, followed by photon counting of the photoluminescent photon and a majority voting to decide the binary outcome. The NV center is reinitialized after each photon counting. During the free evolution in the Ramsey sequence the NV center precesses freely in the external magnetic field, thereby encoding its value in its state. The two possible controls we have on the system are the duration of the free evolution $\tau$ and the phase $\phi$ applied before the photon counting. The resource of the estimation task can be either the total number of measurements or the total evolution time.

Achtung! The model() method must still be implemented in this class. It should describe the probability of getting $+1$ in the measurement after the majority voting from the collected photons.

Constructor of the NVCenter class.

Parameters

batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
params: List[Parameter]: List of unknown parameters to estimate in the NV center experiment, with their respective bounds.
prec{“float64”, “float32”}: Precision of the floating point operations in the simulation.
res: {“meas”, “time”}: Resource type for the present metrological task, can be either the total evolution time, i.e. time, or the total number of measurements on the NV center, i.e. meas.
control_phase: bool = False: If this flag is True, beside the free evolution time, also the phase applied before the photon counting is controlled by the agent.

count_resources(resources: Tensor, controls: Tensor, true_values: Tensor, meas_step: Tensor): The resources can be either the total number of measurements, or the total evolution time, according to the attribute res of the NVCenter class.

perform_measurement(controls: Tensor, parameters: Tensor, meas_step: Tensor, rangen: Generator)

Measurement on the NV center.

The NV center is measured after having evolved freely in the magnetic field for a time specified by the parameter control. The possible outcomes are $+1$ and $-1$ , selected stochastically according to the probabilities $p(\pm 1| \vec{\theta}, \tau)$ , where $\tau$ is the evolution time (the control) and $\vec{\theta}$ the parameters to estimate. This method returns the observed outcomes and their log-likelihood.

Achtung! The model() method must return the probability $p(\pm 1| \vec{\theta}, \tau)$

class NVCenterDCMagnetometry(batchsize: int, params: List[Parameter], prec: Literal['float64', 'float32'] = 'float64', res: Literal['meas', 'time'] = 'meas', invT2: Optional[float] = None)

Bases: NVCenter

Model describing the estimation of a static magnetic field with an NV center used as magnetometer. The spin-spin relaxation time $T_2^{-1}$ can be either known, or be a parameter to estimate. The estimation will be formulated in terms of the precession frequency $\omega$ of the NV center, which is proportional to the magnetic field $B$ .

This physical model and the application of Reinforcement Learning to the estimation of a static magnetic fields have been also studied in the seminal work of Fiderer, Schuff and Braun 1.

1(1,2,3,4,5,6,7): Lukas J. Fiderer, Jonas Schuff, and Daniel Braun PRX Quantum 2, 020303 (2021).

Constructor of the NVCenterDCMagnetometry class.

Parameters

batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
params: List[Parameter]: List of unknown parameters to estimate in the NV center experiment, with their respective bounds.
prec{“float64”, “float32”}: Precision of the floating point operations in the simulation.
res: {“meas”, “time”}: Resource type for the present metrological task, can be either the total evolution time, i.e. time, or the total number of measurements on the NV center, i.e. meas.
invT2: float, optional: If this parameter is specified only the precession frequency $\omega$ is considered as an unknown parameter, while the inverse of the transverse relaxation time $T_2^{-1}$ is fixed to the value invT2. In this case the list params must contain a single parameter, i.e. omega. If no invT2 is specified, it is assumed that it is an unknown parameter that will be estimated along the frequency in the Bayesian procedure. In this case params must contain two objects, the second of them should be the inverse of the transversal relaxation time.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, meas_step: Tensor, num_systems: int = 1) → Tensor

Model for the outcome of a measurement on a NV center subject to free precession in a static magnetic field. The probability of getting the outcome $+1$ is

(59) $p(+1|\omega, T_2, \tau) := e^{-\frac{\tau}{T_2}} \cos^2 \left( \frac{\omega}{2} \tau \right) + \frac{1-e^{-\frac{\tau}{T_2}}}{2} \; .$

The evolution time $\tau$ is controlled by the trainable agent, and $\omega$ is the unknown precession frequency, which is proportional to the magnetic field. The parameter $T_2$ may or may not be an unknown in the estimation, according to the value of the attribute invT2 of the NVCenterDCMagnetometry class.

main()

Runs the same simulations done by Fiderer, Schuff and Braun 1.

The performances of the optimized neural network and static strategies are reported in the following plot, together with other strategies commonly used in the literature. The resources can be the number of measurements or the total evolution time.

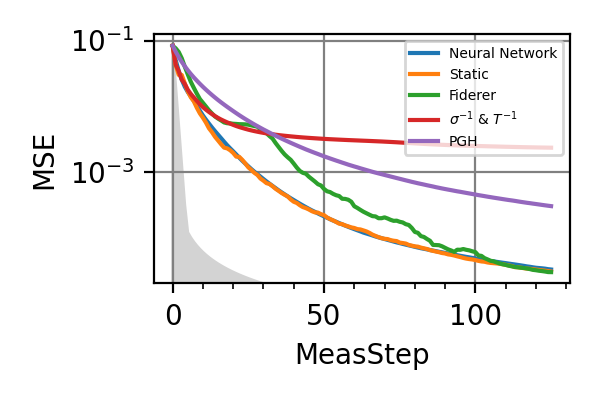
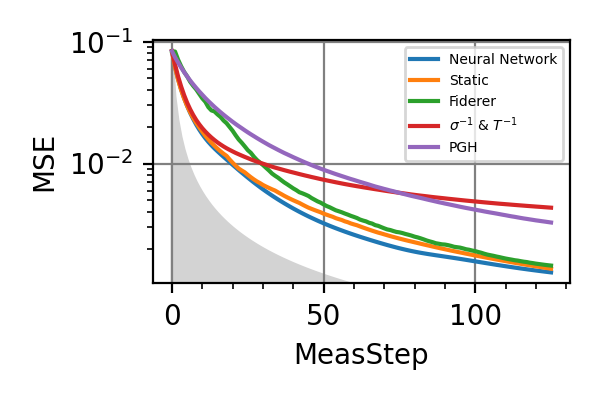
Fig. 1 invT2=0.01, Meas=128	Fig. 2 invT2=0.1, Meas=128
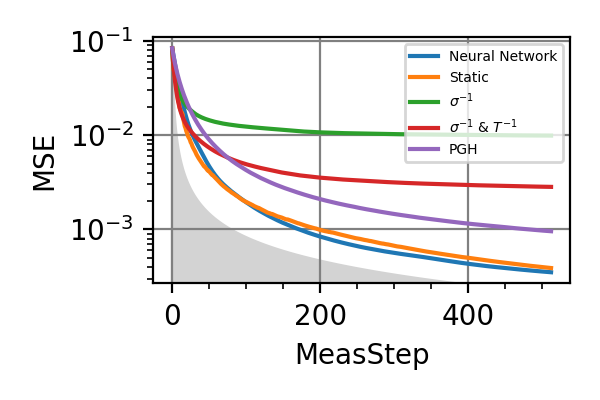
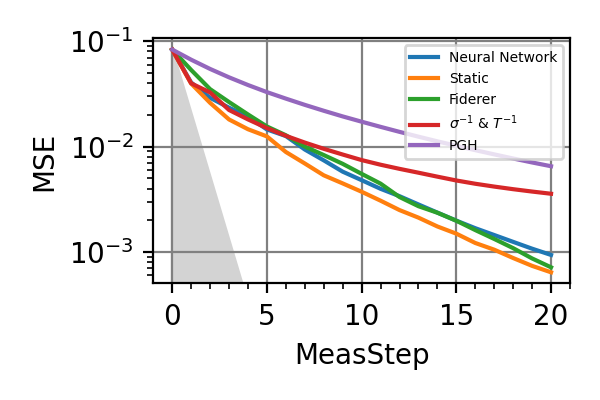
Fig. 3 invT2 in (0.09, 0.11), Meas=512	Fig. 4 invT2=0, Meas=24
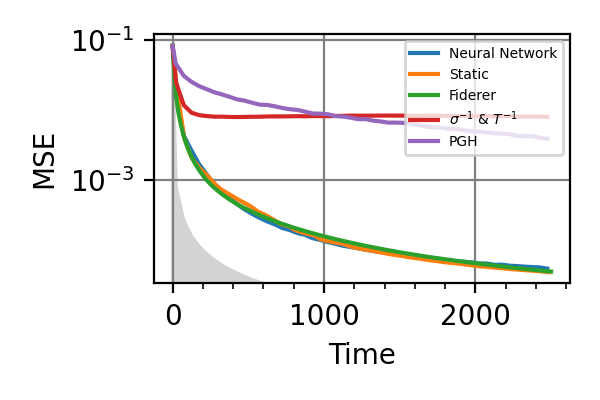
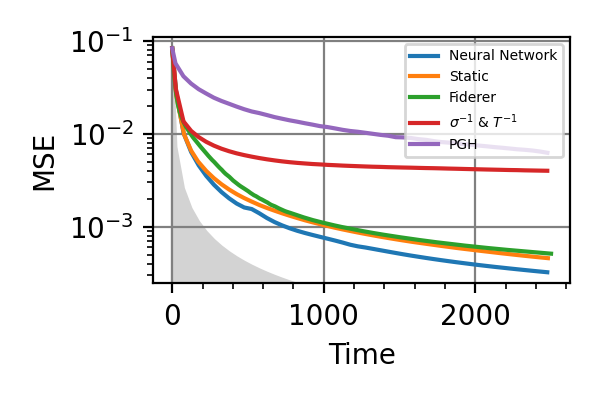
Fig. 5 invT2=0.01, Time=2560	Fig. 6 invT2=0.1, Time=2560
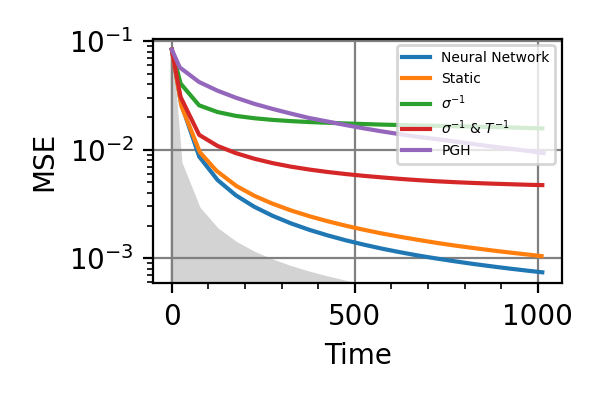
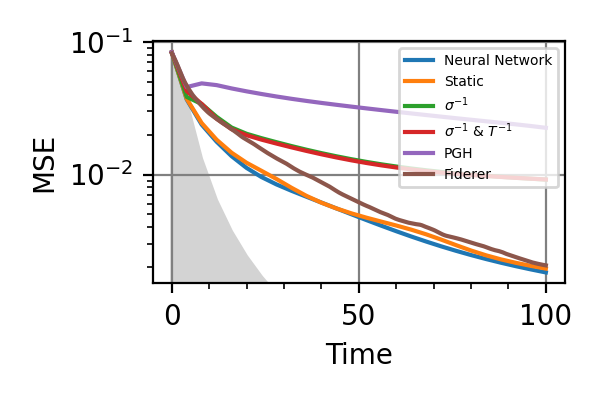
Fig. 7 invT2 in (0.09, 0.11), Time=1024	Fig. 8 invT2=0, Time=128

For the plot referring to the estimation of omega only the green line is the best performance found in the literature so far, obtained in 1 with model-free RL. In the plot corresponding to the simultaneous estimation of both the frequency and the decoherence time we din’t compare our results with 1 and the green line in simply the $\sigma^{-1}$ .

The shaded grey areas in the above plot indicate the Bayesian Cramér-Rao bound, which is the the ultimate precision bound computed from the Fisher information.

From the above plots we can conclude that the adaptive strategy offers no advantage with respect to the optimal static strategy for those experiments limited in the number of measurements and for all those with a sufficiently high coherence time. For $T_2=10$ we see some small advantage of the adaptive strategy in the time limited experiments. This observation is in accordance with the analysis based only on the Fisher information. For $T_2=0$ the Fisher information of a single measurement is $\tau^2$ and is independent on $\omega$ . For $T_2>0$ the Fisher information manifests a dependence on $\omega$ , which could indicate the possibility of an adaptive strategy being useful, which is confirmed in these simulations.

Notes

The results of the simulations with invT2 in (0.09, 0.11) are very similar to that with invT2=0.1 because of the relatively narrow prior on invT2.

For an NV center used as a magnetometer the actual decoherence model is given by $e^{-\left( \frac{\tau}{T_2} \right)^2}$ instead of $e^{-\frac{\tau}{T_2}}$

Achtung! The performances of the time limited estimations with the $\sigma^{-1}$ and the PGH strategies are not in accordance with the results of Fiderer, Schuff and Braun 1. Also the simulations with invT2 in (0.09, 0.11) do not agree with the results reported in this paper.

Normally in the applications the meaningful resource is the total time required for the estimation. This doesn’t coincide however with the total evolution time that we considered, because the initialization of the NV center, the read-out the and the data processing all take time. This overhead time is proportional to the number of measurements, so that in a real experiment we expect the actual resource to be a combination of the evolution time and the number of measurements.

In a future work the role of the higher moments of the posterior distribution in the determination of the controls should be explored. In particular it should be understood if with

(60) $\tau = NN(\hat{\omega}, \hat{\sigma}, \hat{\gamma}_1, \frac{\hat{\mu}_4}{\hat{\sigma}^4}, \frac{\hat{\mu}_5}{\hat{\sigma}^5}, \cdots) \; ,$

more advantage from the adaptivity could be extracted.

In room-temperature magnetometry it is impossible to do single-shot readout of the NV center state (SSR). We should train the control strategy to work with non-SSR, as done by Zohar et al 2

All the trainings of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

2: I Zohar et al, Quantum Sci. Technol. 8 035017 (2023).

parse_args()

Arguments

scratch_dir: str: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./nv_center_dc/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./nv_center_dc/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float32”: Floating point precision of the whole simulation.
n: int = 64: Number of neurons per layer in the neural network.
num_particles: int = 480: Number of particles in the ensemble representing the posterior.
iterations: int = 32768: Number of training steps.
scatter_points: int = 32: Number of points in the Resources/Precision csv produced by performance_evaluation().

static_field_estimation(args, batchsize: int, max_res: float, learning_rate: float = 0.01, gradient_accumulation: int = 1, cumulative_loss: bool = False, log_loss: bool = False, res: Literal['meas', 'time'] = 'meas', invT2: Optional[float] = None, invT2_bound: Optional[Tuple] = None, cov_weight_matrix: Optional[List] = None, omega_bounds: Tuple[float, float] = (0.0, 1.0))

Simulates the Bayesian estimation of a static magnetic field with an NV center, for a neural network controlling the evolution time, a static strategy, two variations of the $\sigma^{-1}$ strategy, and the particle guess heuristic (PGH).

The measurement loop is showed in the following picture.

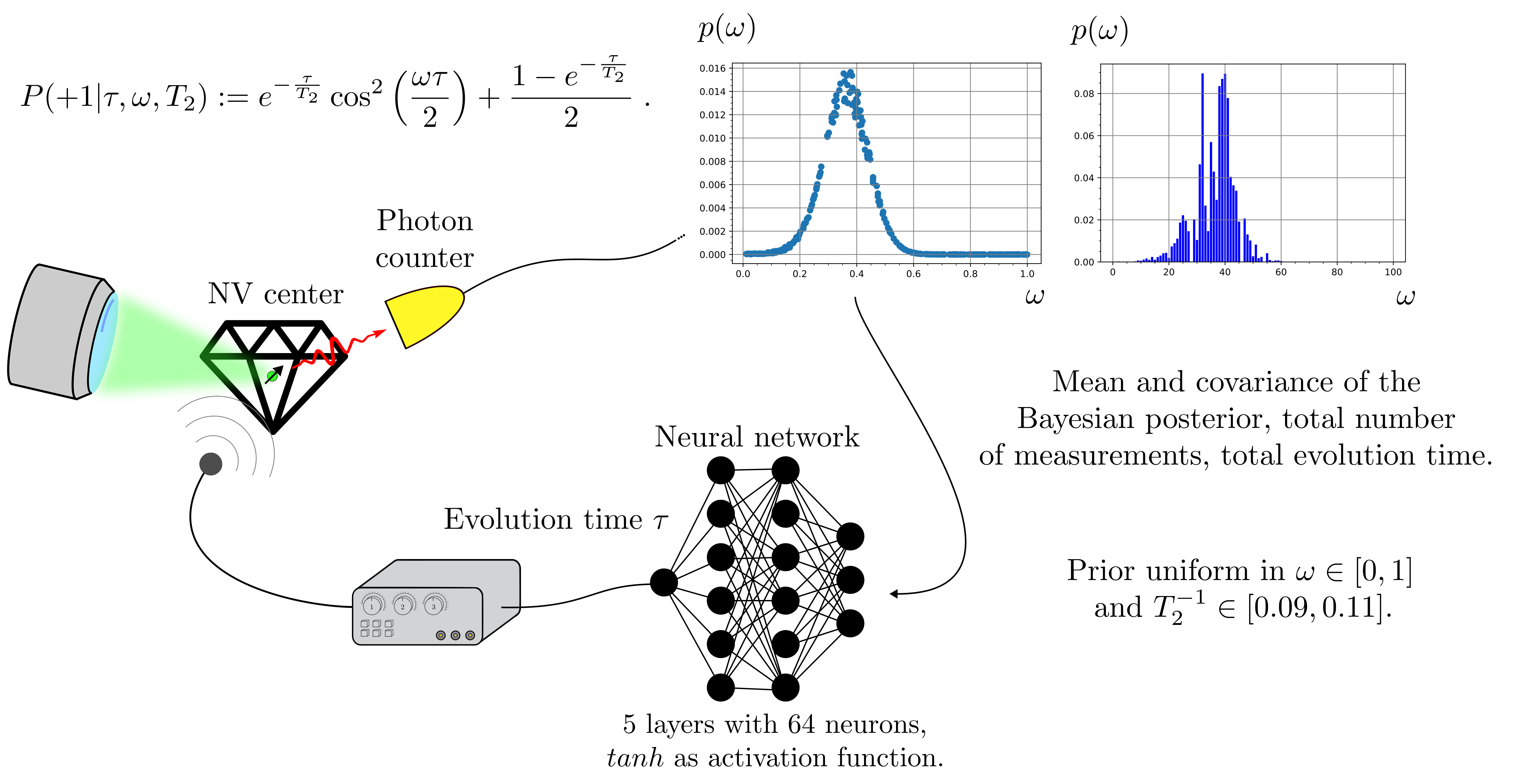
Parameters

args:: Arguments passed to the Python script.
batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
max_res: float: Maximum amount of resources allowed to be consumed in the estimation.
learning_rate: float = 1e-2: Initial learning rate for the neural network. The initial learning rate of the static strategy is fixed to 1e-1. They both decay with InverseSqrtDecay.
gradient_accumulation: int = 1: Flag of the train() function.
cumulative_loss: bool = False: Flag cumulative_loss.
log_loss: bool = False: Flag log_loss.
res: {“meas”, “time”}: Type of resource for the simulation. It can be either the number of measurements or the total evolution time.
invT2: float, optional: Inverse of the transversal relaxation time. If $T_2 = \infty$ or it is unknown and must be estimated, this parameter should not be passed.
invT2_bound: Tuple[float, float], optional: Extrema of the uniform prior for the Bayesian estimation of the inverse of the transversal relaxation time.
cov_weight_matrix: List, optional: Weight matrix for the mean square error on the frequency and on the inverse of the coherence time $T_2$ .
omega_bounds: Tuple[float, float] = (0.0, 1.0): Extrema of admissible values for the precession frequency.

NV center - Phase control

class NVCenterDCMagnPhase(batchsize: int, params: List[Parameter], prec: Literal['float64', 'float32'] = 'float64', res: Literal['meas', 'time'] = 'meas', invT2: Optional[float] = None)

Bases: NVCenter

Model describing the estimation of a static magnetic field with an NV center used as magnetometer. The transversal relaxation time $T_2^{-1}$ can be either known, or be a parameter to estimate. The estimation will be formulated in terms of the precession frequency $\omega$ of the NV center, which is proportional to the magnetic field $B$ . With respect to the nv_center_dc module we add here the possibility of imprinting an arbitrary phase on the NV-center state before the photon counting measurement.

Constructor of the NVCenterDCMagnPhase class.

Parameters

batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
params: List[Parameter]: List of unknown parameters to estimate in the NV center experiment, with their respective bounds. This contains either the precession frequency only or the frequency and the inverse coherence time.
prec{“float64”, “float32”}: Precision of the floating point operations in the simulation.
res: {“meas”, “time”}: Resource type for the present metrological task, can be either the total evolution time, i.e. time, or the total number of measurements on the NV center, i.e. meas.
invT2: float, optional: If this parameter is specified only the precession frequency $\omega$ is considered as an unknown parameter, while the inverse of the transverse relaxation time $T_2^{-1}$ is fixed to the value invT2. In this case the list params must contain a single parameter, i.e. omega. If no invT2 is specified, it is assumed that it is an unknown parameter that will be estimated along the frequency in the Bayesian procedure. In this case params must contain two objects, the second of them should be the inverse of the transversal relaxation time.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, meas_step: Tensor, num_systems: int = 1) → Tensor

Model for the outcome of a measurement on a NV center that has been precessing in a static magnetic field. The probability of getting the outcome $+1$ is

(61) $p(+1|\omega, T_2, \tau) := e^{-\frac{\tau}{T_2}} \cos^2 \left( \frac{\omega}{2} \tau + \phi \right) + \frac{1-e^{-\frac{\tau}{T_2}}}{2} \; .$

The evolution time $\tau$ and the phase $\phi$ are controlled by the trainable agent, and $\omega$ is the unknown precession frequency, which is proportional to the magnetic field. The parameter $T_2$ may or may not be an unknown in the estimation, according to the value of the attribute invT2 of the NVCenterDCMagnPhase class.

main()

Runs the same simulations done by Fiderer, Schuff and Braun 1 but with the possibility of controlling the phase of the NV center before the Ramsey measurement.

The performances of the optimized neural network and the static strategy are reported in the following plots, together with other strategies commonly used in the literature. The resource can be either the total number of measurements or the total evolution time. Beside the NN optimized to control $\tau$ and $\phi$ , the performances of the NN trained to control only the evolution time $\tau$ are reported in brown.

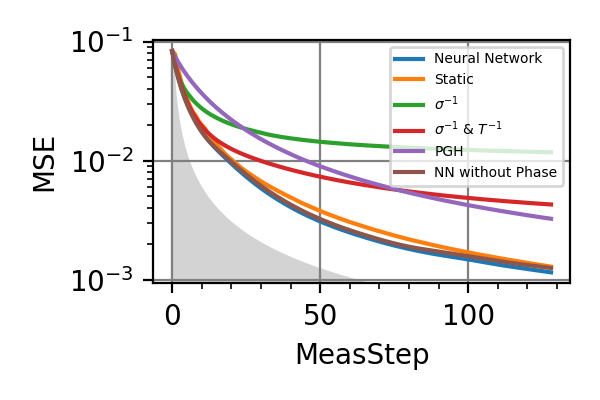
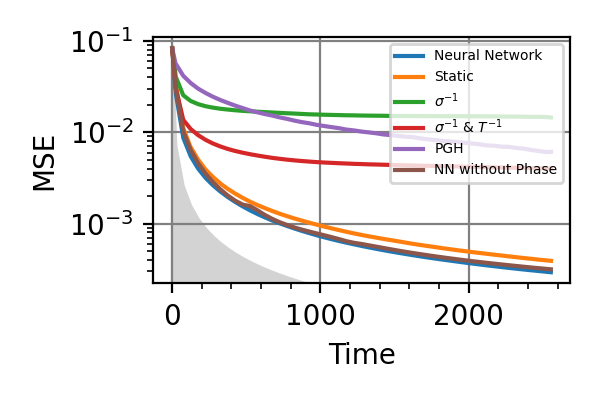
Fig. 9 invT2=0.1, Meas=128	Fig. 10 invT2=0.1, Time=2560
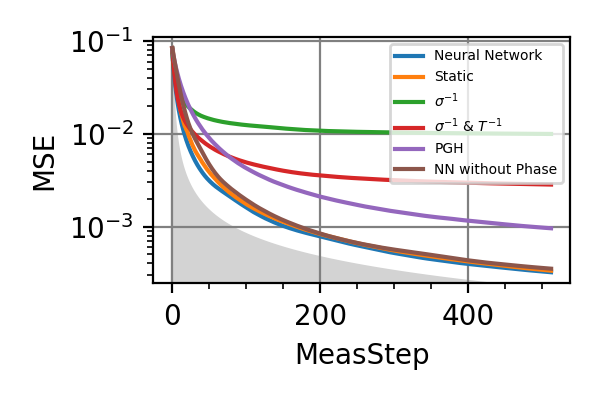
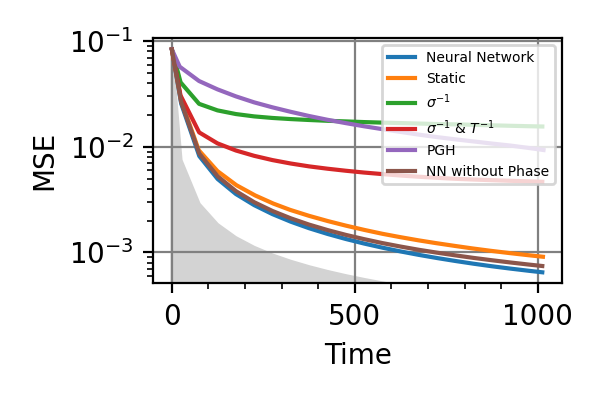
Fig. 11 invT2 in (0.09, 0.11), Meas=512	Fig. 12 invT2 in (0.09, 0.11), Time=1024
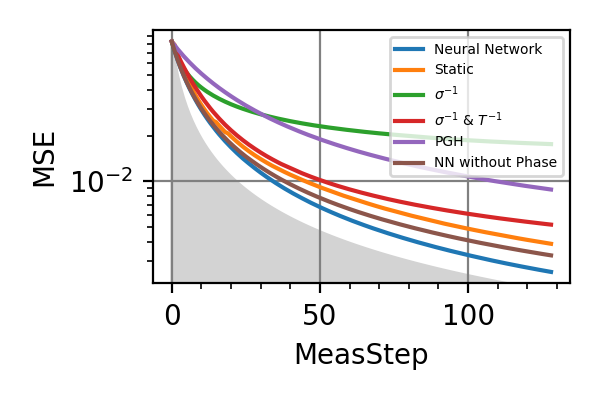
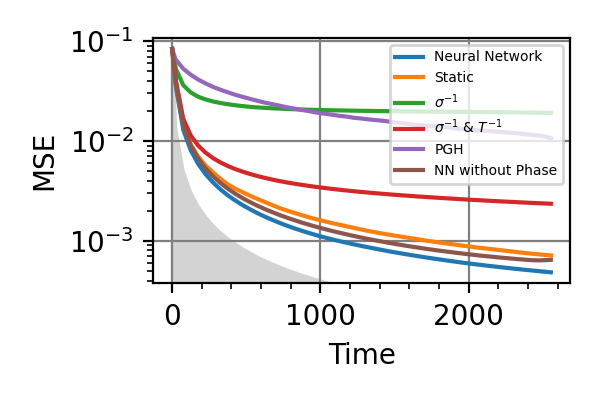
Fig. 13 invT2=0.2, Meas=128	Fig. 14 invT2=0.2, Time=2560

The shaded grey areas in the above plot indicate the Bayesian Cramér-Rao bound, which is the the ultimate precision bound computed from the Fisher information.

There is only a very small advantage in controlling the phase for $T_2^{-1} = 0.1$ , if there is any at all. Similarly, with $T_2^{-1} = 0, 0.01$ no advantage has been found. For $T_2^{-1} = 0.1$ and Time=2560 the phase control had converged to $\phi=\pi$ , and more training could not take it out of this minimum. For $T_2^{-1} = 0.2$ the advantage in introducing also the phase control becomes more consistent.

Notes

For the phase control be advantageous, the phase $\omega \tau$ must be known to some extent. While the error on $\omega$ goes down, the evolution time increases, so that the error on $\omega \tau$ doesn’t go to zero. This limits the utility of controlling the phase in DC magnetometry.

All the training of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

parse_args()

Arguments

scratch_dir: str: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./nv_center_dc_phase/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./nv_center_dc_phase/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float32”: Floating point precision of the whole simulation.
n: int = 64: Number of neurons per layer in the neural network.
num_particles: int = 480: Number of particles in the ensemble representing the posterior.
iterations: int = 32768: Number of training steps.
scatter_points: int = 32: Number of points in the Resources/Precision csv produced by performance_evaluation().

Simulates the Bayesian estimation of a static magnetic field with an NV center, for a neural network controlling the sensor, a static strategy, two variations of the $\sigma^{-1}$ strategy, and the particle guess heuristic (PGH). Beside the evolution time also the phase is be controlled by the agent.

Parameters

args:: Arguments passed to the Python script.
batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
max_res: float: Maximum amount of resources allowed to be consumed in the estimation.
learning_rate: float = 1e-2: Initial learning rate for the neural network. The initial learning rate of the static strategy is fixed to 1e-1. They both decay with InverseSqrtDecay.
gradient_accumulation: int = 1: Flag of the train() function.
cumulative_loss: bool = False: Flag cumulative_loss.
log_loss: bool = False: Flag log_loss.
res: {“meas”, “time”}: Type of resource for the simulation. It can be either the number of Ramsey measurements or the total evolution time.
invT2: float, optional: Inverse of the transversal relaxation time. If $T_2 = \infty$ or it is unknown and must be estimated, this parameter should not be passed.
invT2_bound: Tuple[float, float], optional: Extrema of the uniform prior for the Bayesian estimation of the inverse of the transversal relaxation time.
cov_weight_matrix: List, optional: Weight matrix for the mean square error on the frequency and on the inverse of the coherence time $T_2$ .
omega_bounds: Tuple[float, float] = (0.0, 1.0): Extrema of admissible values for the precession frequency.

NV center - AC Magnetometry

class NVCenterACMagnetometry(batchsize: int, params: List[Parameter], omega: float = 0.2, prec: Literal['float64', 'float32'] = 'float64', res: Literal['meas', 'time'] = 'meas', invT2: Optional[float] = None)

Bases: NVCenter

This model describes the estimation of the intensity of oscillating magnetic field of known frequency with an NV center used as magnetometer. The transversal relaxation time $T_2$ can be either known, or be a parameter to estimate.

Constructor of the NVCenterACMagnetometry class.

Parameters

batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
params: List[Parameter]: List of unknown parameters to estimate in the NV center experiment, with their respective bounds. This contains either the field intensity $B$ only or $B$ and the inverse coherence time $T_2^{-1}$ .
omega: float = 0.2: Frequency of the oscillating magnetic field to be estimated.
prec{“float64”, “float32”}: Precision of the floating point operations in the simulation.
res: {“meas”, “time”}: Resource type for the present metrological task, can be either the total evolution time, i.e. time, or the total number of measurements on the spin, i.e. meas.
invT2: float, optional: If this parameter is specified the estimation is performed only for the field intensity $B$ while the inverse of the transverse relaxation time $T_2^{-1}$ is fixed to the value invT2. In this case the list params must contain a single parameter. If no invT2 is specified, it is assumed that it is an unknown parameter that will be estimated along $B$ by the Bayesian procedure. In this case params must contain two objects, the second of them should be the inverse of the transversal relaxation time.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, meas_step: Tensor, num_systems: int = 1)

Model for the outcome of a measurement on a spin that has been precessing in an oscillating magnetic field of intensity $B$ and known frequency omega. The probability of getting the outcome $+1$ is

(62) $p(+1|B, T_2, \tau) := e^{-\frac{\tau}{T_2}} \cos^2 \left[ \frac{B}{2 \omega} \sin( \omega \tau) \right] + \frac{1-e^{-\frac{\tau}{T_2}}}{2} \; .$

The evolution time $\tau$ is controlled by the trainable agent, and $B$ is the unknown magnetic field. The parameter $T_2$ may or may not be an unknown in the estimation, according to the value of the attribute invT2 of the NVCenterACMagnetometry class.

alternate_field_estimation(args, batchsize: int, max_res: float, learning_rate: float = 0.01, gradient_accumulation: int = 1, cumulative_loss: bool = False, log_loss: bool = False, res: Literal['meas', 'time'] = 'meas', omega: float = 0.2, invT2: Optional[float] = None, invT2_bound: Optional[Tuple] = None, cov_weight_matrix: Optional[List] = None, B_bounds: Tuple[float, float] = (0.0, 1.0))

Simulates the Bayesian estimation of the intensity of an oscillating magnetic field of known frequency with an NV center sensor, for a neural network controlling the evolution time, a static strategy, two variations of the $\sigma^{-1}$ strategy, and the particle guess heuristic (PGH).

The measurement loop is showed in the following picture.

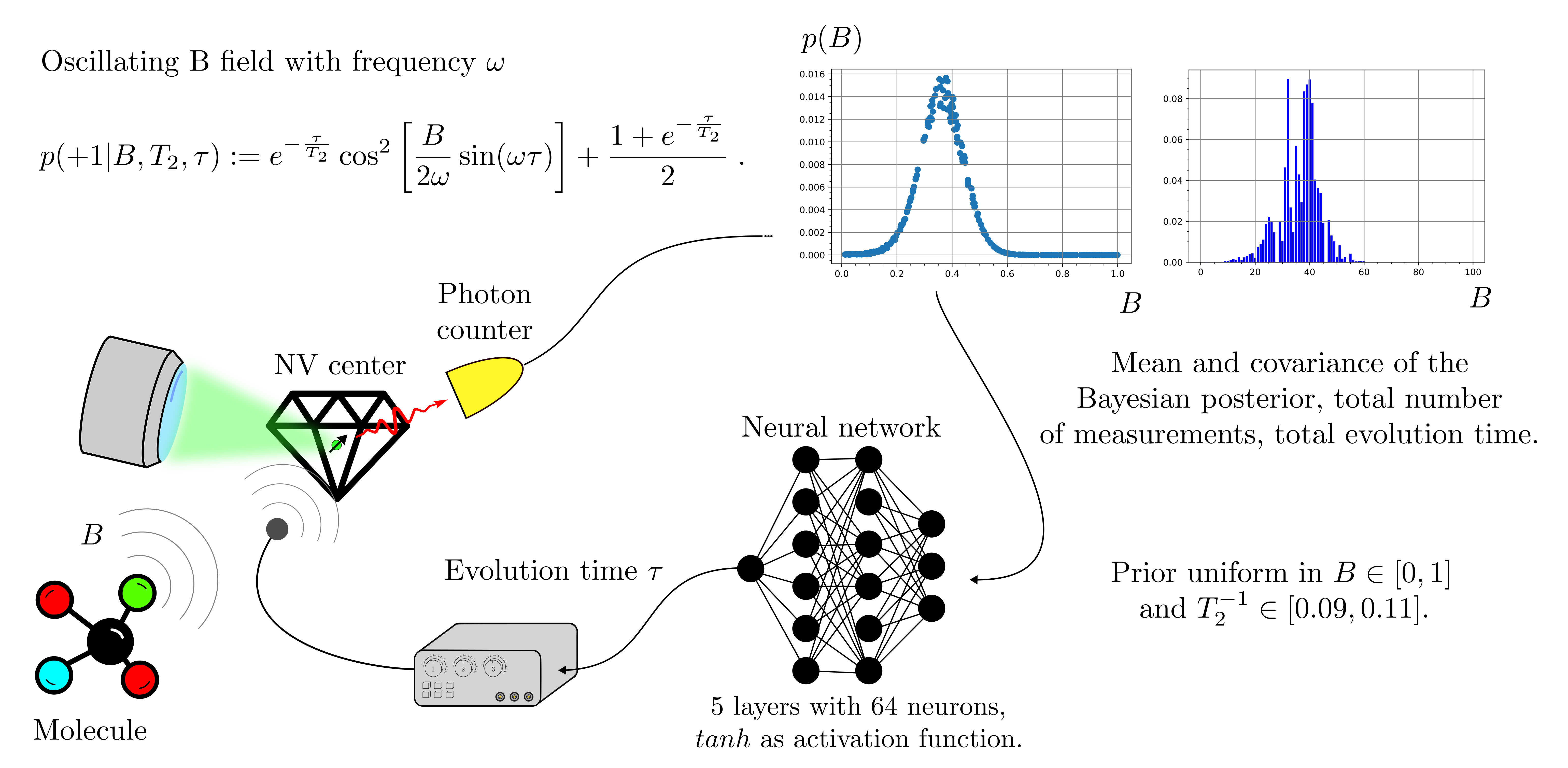
Parameters

args:: Arguments passed to the Python script.
batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
max_res: float: Maximum amount of resources allowed to be consumed in the estimation.
learning_rate: float = 1e-2: Initial learning rate for the neural network. The initial learning rate of the static strategy is fixed to 1e-1. They both decay with InverseSqrtDecay.
gradient_accumulation: int = 1: Flag of the train() function.
cumulative_loss: bool = False: Flag cumulative_loss.
log_loss: bool = False: Flag log_loss.
res: {“meas”, “time”}: Type of resource for the simulation. It can be either the number of measurements or the total evolution time.
omega: float = 0.2: Known frequency of the oscillating magnetic field.
invT2: float, optional: Inverse of the transversal relaxation time. If it is infinity or it is unknown and must be estimated, this parameter should not be passed.
invT2_bound: Tuple[float, float], optional: Extrema of admissible values of the inverse of the transversal relaxation time, whose precise value is not known before the estimation.
cov_weight_matrix: List, optional: Weight matrix for the mean square error on the field intensity and on the decoherence parameter.
B_bounds: Tuple[float, float] = (0.0, 1.0): Extrema of admissible values for the intensity of the magnetic field.

main()

Runs the simulations for the estimation of the intensity of an oscillating magnetic field of known frequency, for the same parameters of the simulations done by Fiderer, Schuff and Braun 1,

The performances of the optimized neural network and static strategies are reported in the following plots, together with the simulated $\sigma^{-1}$ and PGH strategies, for a range of resources and coherence times. The resource can be either the total evolution time or the total number of measurements.

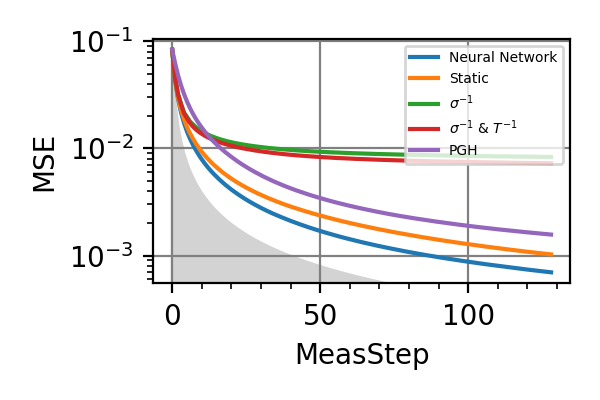
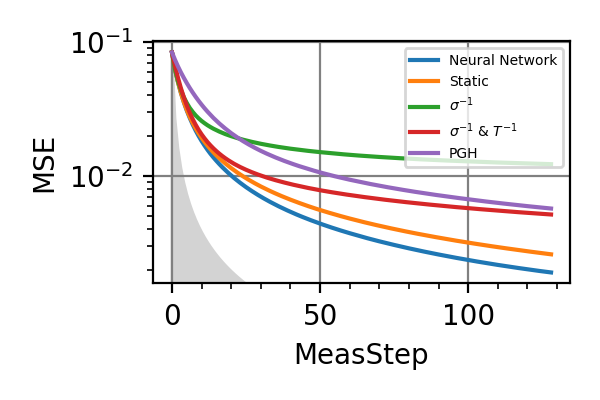
Fig. 15 invT2=0.01, Meas=128	Fig. 16 invT2=0.1, Meas=128
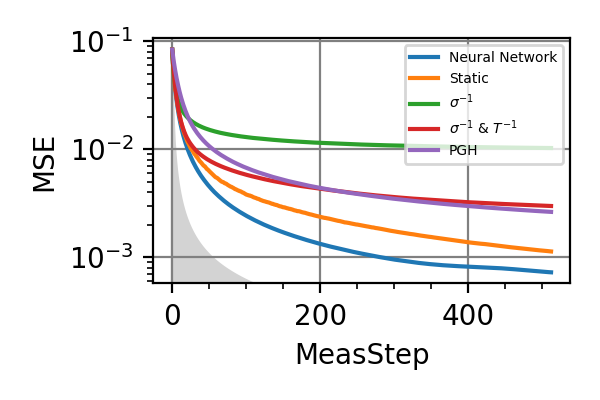
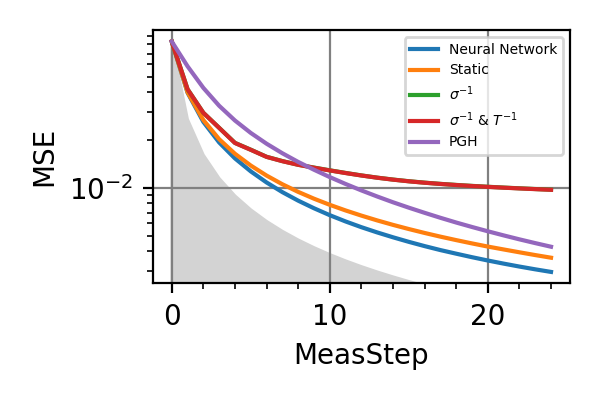
Fig. 17 invT2 in (0.09, 0.11), Meas=512	Fig. 18 invT2=0, Meas=24
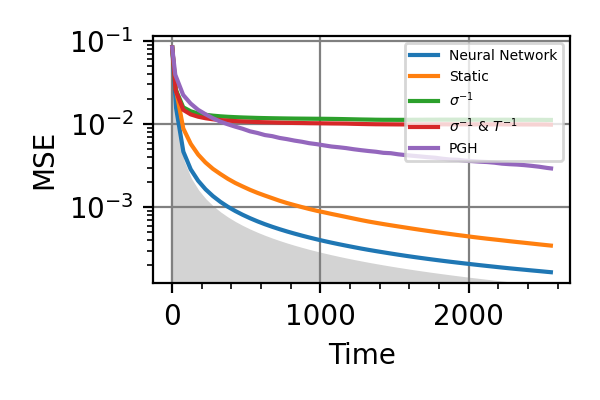
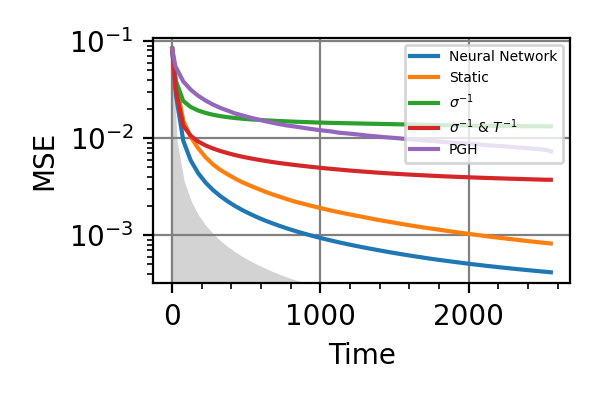
Fig. 19 invT2=0.01, Time=2560	Fig. 20 invT2=0.1, Time=2560
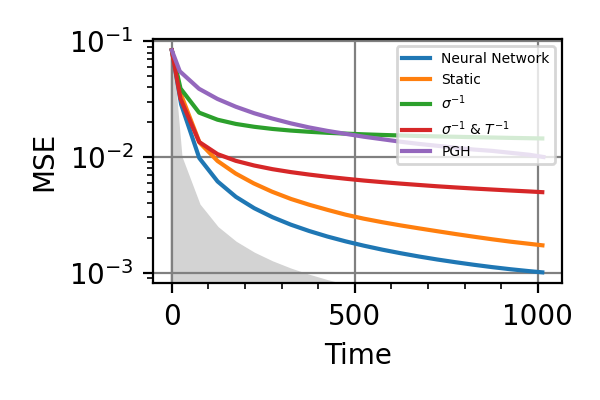
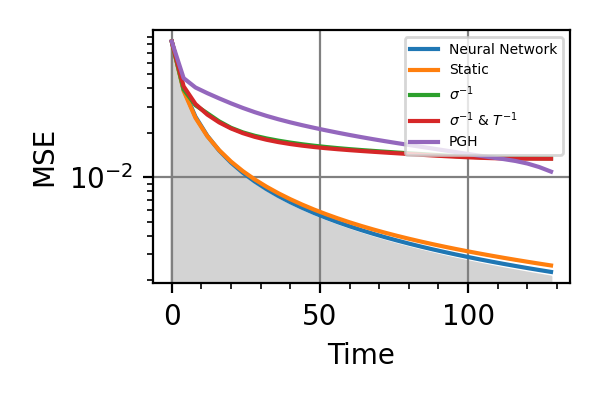
Fig. 21 invT2 in (0.09, 0.11), Time=1024	Fig. 22 invT2=0, Time=128

The shaded grey areas in the above plot indicate the Bayesian Cramér-Rao bound, which is the the ultimate precision bound computed from the Fisher information.

In all simulations we see that an “adaptivity-gap” opens between the precision of the static and the NN strategies as the resources grow.

Notes

The model used in this example is formally equivalent to that of the nv_center_dc module, where the adaptive strategy gives only small advantages, at difference with the results obtained hare for AC-magnetometry. This is because the AC model maps to the DC one in a very different region of parameters with respect to the region we have explored in nv_center_dc.

In AC magnetometry the technique of dynamical decoupling (DD) is often used to improve the sensitivity with respect to $B$ and to increase the coherence time $T_2$ . This consists in series of $\pi$ -pulses that reverse the sign of the accumulated phase. Given $t_i, \, 0<i<N+1$ the times at which the instantaneous $\pi$ -pulse are applied, the outcome probability for a noiseless estimation is given by

(63) $p(0|B, T_2, \lbrace t_i \rbrace) = \cos^2 \left[ \frac{B}{2 \omega} \sum_{i=1}^{N+1} (-1)^i \left[ \sin(\omega t_{i})- \sin(\omega t_{i-1}) \right] \right] \; ,$

with $N$ being the number of pulses, and $t_0$ and $t_{N+1}$ being respectively the initialization and the measurement times.

In the simulations done we have used no $\pi$ -pulse, but optimizing their application is the natural extension of this example, left for future works. For controlling the pulses there are possibilities:

the interval between the pulses is fixed to $\tau = t_{i+1}-t_i$ , which is produced by a NN together with the number of pulses N,
the controls are the $N$ time intervals $\tau_i = t_{i}-t_{i-1}$ . The number of pulses is fixed but they can be made ineffective with $\tau_i = 0$ ,
the control is the free evolution time $\tau$ together with a boolean variable, that tells whether a pulse or a measurement has to be applied after the free evolution. This would require a stateful model for the NV center, where the current phase is the state.

The problem of estimating $B$ knowing the frequency is complementary to the protocol for the optimal discrimination of frequencies presented in 3, which is used to distinguish chemical species in a sample. In this work the authors put forward an optimal strategy for the discrimination of two frequencies $\omega$ and $\omega+\Delta \omega$ , knowing the intensity $B$ . If $\Delta \omega \ll \omega$ and the field intensity is unknown a two stage approach to the problem is possible. We can estimate $B$ as done in this example, i.e. by considering the frequency fixed to $\omega$ , and then proceed with the optimal frequency discrimination based on the intensity just estimated. The error probability of the second stage depends on the precision of the first. Given a fixed total time for the discrimination, the time assigned to the first and the second stage can be optimized to minimize the final error. For close frequencies we expect this two stage protocol to be close to optimality. A small improvement would be to simulate the estimation of $B$ with the frequency as a nuisance parameters. It is important for the first stage, the estimation of the field intensity, to have low sensitivity to variations in the frequency. For optimizing frequency discrimination with $B$ as a nuisance parameter in a fully integrated protocol the introduction of $\pi$ -pulses is necessary, just like for dynamical decoupling. The natural extension of hypothesis testing on the frequency is the estimation of both the intensity and the frequency of the magnetic field optimally, both starting from a broad prior. All these improvements are left for future work.

All the training of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

3: Schmitt, S., Gefen, T., Louzon, D. et al. npj Quantum Inf 7, 55 (2021).

parse_args()

Arguments

scratch_dir: str, required: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./nv_center_ac/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./nv_center_ac/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float32”: Floating point precision of the whole simulation.
n: int = 64: Number of neurons per layer in the neural network.
num_particles: int = 480: Number of particles in the ensemble representing the posterior.
iterations: int = 32768: Number of training steps.
scatter_points: int = 32: Number of points in the Resources/Precision csv produced by performance_evaluation().

NV center - Hyperfine coupling

class NVCenterHyperfine(batchsize: int, params: List[Parameter], prec: Literal['float64', 'float32'] = 'float64', res: Literal['meas', 'time'] = 'meas', invT2: float = 0.0)

Bases: NVCenter

This class models the measurement of an NV center strongly coupled to a 13C nuclear spin in the diamond lattice. Such nuclear spin is not hidden in the spin bath of nuclei, that causes the dephasing noise, instead it splits the energy levels of the NV center, according to the hyperfine interaction strength. The precession frequency of the NV center in a magnetic field is determined by the state of the nuclear spin. In the work of T. Joas et al. 4 multiple incoherent nuclear spin flips happen during the read out, so that the nuclear spin is in each eigenstate approximately half of the time. This motivates the choice for the outcome probability of Ramsey measure on the NV center:

(64) $\begin{aligned} p(+1|\omega_0, \omega_1, T_2, \tau) := \frac{e^{-\frac{\tau}{T_2}}}{2} & \left[ \cos^2 \left( \frac{\omega_0 \tau}{2} + \phi \right) \right. \\ & \left. + \cos^2 \left( \frac{\omega_1 \tau}{2} + \phi\right) \right] + \frac{1-e^{-\frac{\tau}{T_2}}}{2} \; . \end{aligned}$

In such model $\omega_0$ and $\omega_1$ are the two precession frequencies of the sensor to be estimated, splitted by the hyperfine interaction, $T_2$ is the coherence time, $\tau$ and $\phi$ are the controls, being respectively the evolution time and the phase.

Notes

This models is completely symmetric under permutation of the two precession frequencies. In these cases the flag permutation_invariant must be activated. Only those weight matrices that are permutationally invariant should be considered for the estimation.

All the training of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

4: Joas, T., Schmitt, S., Santagati, R. et al. npj Quantum Inf 7, 56 (2021).

Constructor of the NVCenterHyperfine class.

Parameters

batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
params: List[Parameter]: List of unknown parameters to estimate in the NV center experiment, with their respective bounds. These are the two precession frequencies $\omega_0$ and $\omega_1$ .
prec{“float64”, “float32”}: Precision of the floating point operations in the simulation.
res: {“meas”, “time”}: Resource type for the present metrological task, can be either the total evolution time, i.e. time, or the total number of measurements on the NV center, i.e. meas.
invT2: float = 0.0: The inverse of the transverse relaxation time $T_2^{-1}$ is fixed to the value invT2.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, meas_step: Tensor, num_systems: int = 1) → Tensor: Model for the outcome probability of the NV center subject to the hyperfine interaction with the carbon nucleus and measured through photoluminescence after a Ramsey sequence. The probability of getting +1 in the majority voting following the photon counting is given by Eq.64.

Notes

There is also another way of expressing the outcome probability of the measurement. Instead of defining the model in terms of $\omega_0$ and $\omega_1$ we could define it in terms of the frequency sum $\Sigma = \omega_0 + \omega_1$ and frequency difference $\Delta = \omega_1 - \omega_0$ , thus writing

(65) $\begin{aligned} p(+1|\Sigma, \Delta, T_2, \tau) := \frac{e^{-\frac{\tau}{T_2}}}{2} & \left[ \cos^2 \left( \frac{\Sigma+\Delta}{4} \tau + \phi \right) \right. \\ & \left. + \cos^2 \left( \frac{\Sigma-\Delta}{4} \tau + \phi\right) \right] + \frac{1-e^{-\frac{\tau}{T_2}}}{2} \; . \end{aligned}$

In this form there is no permutational invariance in $\Sigma$ and $\Delta$ , instead the model is invariant under the transformation $\Delta \rightarrow - \Delta$ . We should choose a prior having $\Delta>0$ , which means $\omega_1>\omega_0$ . We could impose the positivity of the frequencies by requiring $\Sigma>\Delta$ in the prior.

hyperfine_parallel_estimation(args, batchsize: int, max_res: float, learning_rate: float = 0.01, gradient_accumulation: int = 1, cumulative_loss: bool = False, log_loss: bool = False, res: Literal['meas', 'time'] = 'meas', invT2: Optional[float] = None, cov_weight_matrix: Optional[List] = None, omega_bounds: Tuple[float, float] = (0.0, 1.0)): Estimation of the frequencies of two hyperfine lines in the spectrum of an NV center strongly interacting with a 13C nuclear spin. The mean square errors of the two parameters are weighted equally with $G=\text{Id}$ . The frequency difference is the component of the hyperfine interaction parallel to the NV center quantization axis, i.e. $A_{||} = | \omega_1 - \omega_0 |$ . The priors for $\omega_0$ and $\omega_1$ are both uniform in (0, 1), and they are symmetrized. Beside the NN and the static strategies, the performances of the particle guess heuristic (PGH), and of the $\sigma^{-1}$ strategies are reported in the plots. These other strategies are explained in the documentation of the Magnetometry class. The picture represent a schematic of the estimation of the hyperfine coupling controlled by the NN.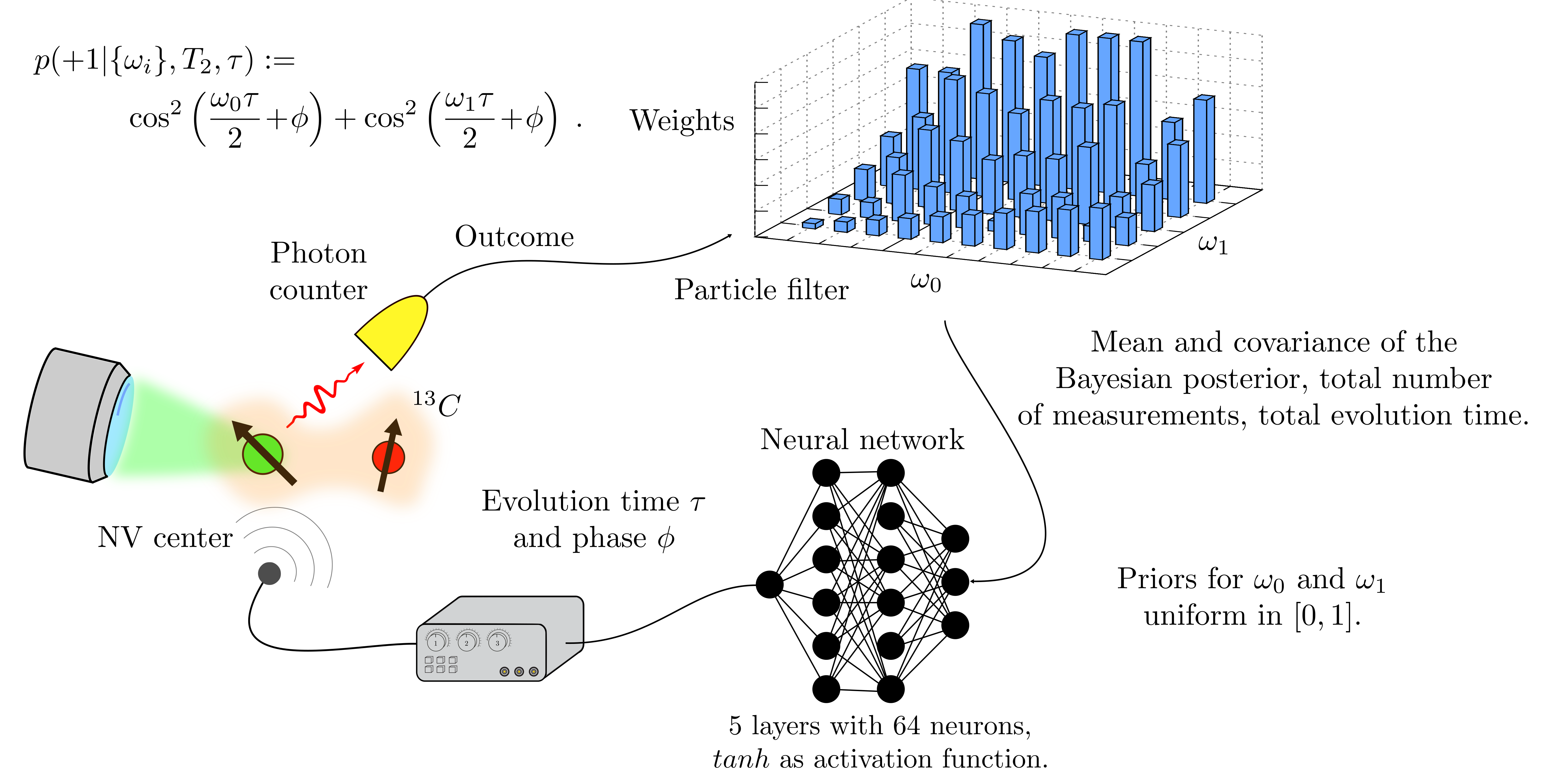

main()

In the following we report the mean square error on the Bayesian estimators for the two frequencies for different strategies and different coherence times $T_2$ . The resource is either the total evolution time or the number of measurements on the NV center.

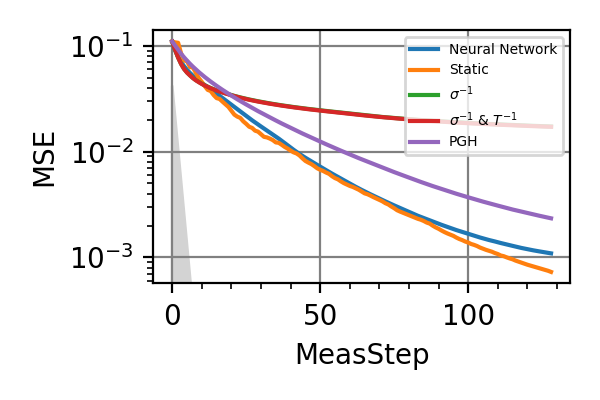
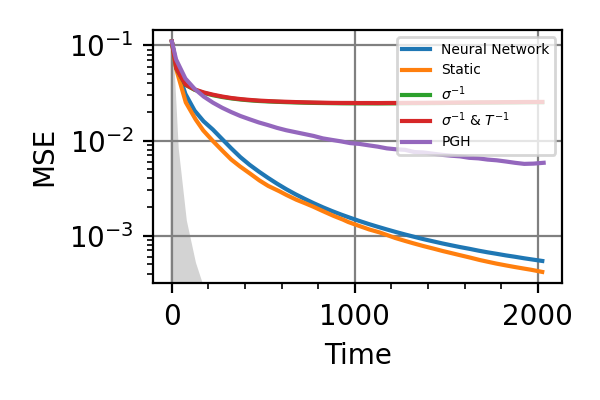
Fig. 23 invT2=0, Meas=128	Fig. 24 invT2=0, Time=2048
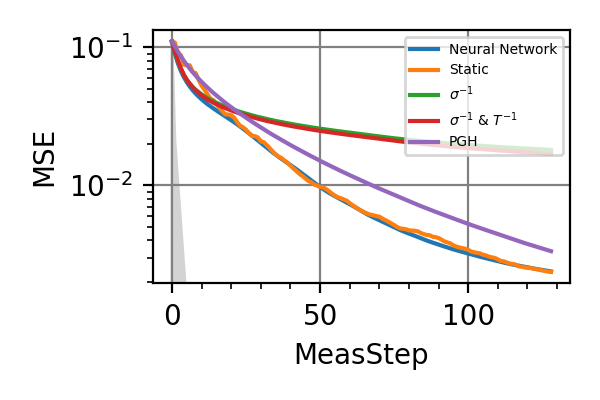
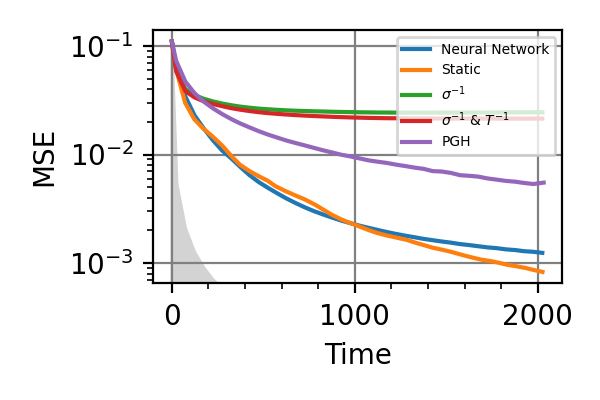
Fig. 25 invT2=0.01, Meas=128	Fig. 26 invT2=0.01, Time=2048
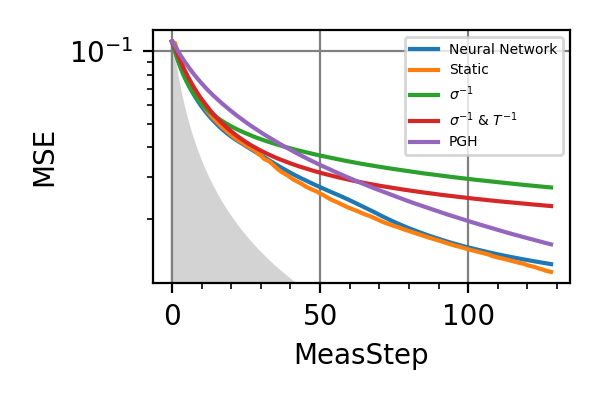
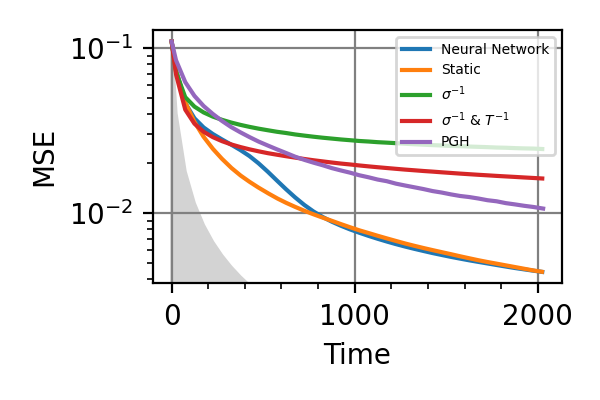
Fig. 27 invT2=0.1, Meas=128	Fig. 28 invT2=0.1, Time=2048

The shaded grey areas in the above plot indicate the Bayesian Cramér-Rao bound, which is the the ultimate precision bound computed from the Fisher information.

From these simulations there seems to be no significant advantage in using an adaptive strategy for the simultaneous estimation of the two precession frequencies. Neither for large nor for small coherence times $T_2$ .

Notes

In a future work the alternative model of Eq.65 should be implemented. Being interested in the difference $\Delta$ , the sum of the frequencies would be treated as a nuisance parameter.

The absence on an advantage of the adaptive strategy over the non-adaptive one is probably also due to the hyper-simplified information passed to the neural network. We are in fact approximating a complex 2D posterior, with many peaks and valleys with a Gaussian. A better approach would be to train an autoencoder to compress the information contained in the posterior and pass it to the NN. The autoencoder will be trained to compress that class of distribution which are produced by the likelihood of the double precession frequency model.

All the simulations of this module have been done on a GPU NVIDIA GeForce RTX-4090-24GB.

parse_args()

Arguments

scratch_dir: str: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./nv_center_double/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./nv_center_double/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float32”: Floating point precision of the whole simulation.
n: int = 64: Number of neurons per layer in the neural network.
num_particles: int = 4096: Number of particles in the ensemble representing the posterior.
iterations: int = 4096: Number of training steps.

NV center - Decoherence

class DecoherenceSimulation(particle_filter: ParticleFilter, phys_model: NVCenterDecoherence, control_strategy: Callable, simpars: SimulationParameters, cov_weight_matrix: Optional[List] = None, random: bool = False, median: bool = False, loss_normalization: bool = False)

Bases: StatelessMetrology

This class does the same job of StatelessMetrology, but it can append a randomly generated control time to the input_strategy Tensor produced by the generate_input() method and it can compute the median square error (MedianSE) instead of the mean square error (MSE) in the loss_function() method.

Parameters passed to the constructor of the DecoherenceSimulation class.

Parameters

particle_filter: ParticleFilter

Particle filter responsible for the update of the Bayesian posterior on the parameters.

phys_model: NVCenterDecoherence

Abstract description of the NC center for the characterization of the dephasing noise.

control_strategy: Callable

Callable object (normally a function or a lambda function) that computes the values of the controls for the next measurement from the Tensor input_strategy, which is produced by the method generate_input().

simpars: SimulationParameters

Contains the flags and parameters that regulate the stopping condition of the measurement loop and modify the loss function used in the training.

cov_weight_matrix: List, optional

Positive semidefinite weight matrix. If this parameter is not passed then the default weight matrix is the identity, i.e. $G=\text{Id}$ .

random: bool = False

If this flag is True then a randomly chosen evolution time $\tau_r$ is added to the input_strategy Tensor produced by generate_input().

median: bool = False

If this flag is True, then instead of computing the mean square error (MSE) from a batch of simulation the median square error (MedianSE) is computed. See the documentation of the loss_function() method.

Achtung! The median can be used in the training, however it means throwing away all the simulations in the batch except to the one that realizes the median. This is not an efficient use of the simulations in the training. When used the median should be always confined to the performances evaluation, while the training is to be carried out with the mean square error.

loss_normalization: bool = False

If loss_normalization is True, then the loss is divided by the normalization factor

(66) $\eta = \min \left( \sum_{i=1}^d G_{ii} \frac{(b_i-a_i)}{12}, \frac{1}{T} \right) \; ,$

Achtung! This flag should be used only if the resource is the total estimation time.

generate_input(weights: Tensor, particles: Tensor, meas_step: Tensor, used_resources: Tensor, rangen: Generator): This method returns the same input_strategy Tensor of the generate_input() method, but, if the attribute random is True, an extra column is appended to this Tensor containing the randomly generated evolution time $\tau_r$ . The value of $\tau_r^{-1}$ is uniformly extracted in the interval of the admissible values for the inverse of the coherence time $T^{-1}$ .

loss_function(weights: Tensor, particles: Tensor, true_values: Tensor, used_resources: Tensor, meas_step: Tensor)

Computes the loss for each estimation in the batch.

If median is False, then it returns the same loss of the loss_function method, i.e. the square error for each simulation in the batch, called $\ell (\omega_k, \vec{\lambda})$ , where $k$ runs from $0$ to $B$ , with $B$ the batchsize. If the flag median is True, this method returns the median square error of the batch, in symbols $\text{Median} [ \ell (\omega_k, \vec{\lambda})]$ . In order to compute it, the vector of losses $\ell (\omega_k, \vec{\lambda})$ is sorted, the element at position $\lfloor B/2 \rfloor$ is then the median of the losses in the batch. Calling $k_0$ the position in the unsorted batch of the simulation realizing the median, the outcome of this method is the vector

(67) $\ell' (\omega_k, \vec{\lambda}) = B \delta_{k, k_0} \text{Median} [ \ell (\omega_k, \vec{\lambda})] \; .$

The advantage of using the median error is the reduced sensitivity to outliers with respect to the mean erro.

Achtung! Even if the performances evaluation can be performed with the median square error, the training should always minimize the mean square error.

class NVCenterDecoherence(batchsize: int, params: List[Parameter], prec: Literal['float64', 'float32'] = 'float64', res: Literal['meas', 'time'] = 'meas')

Bases: NVCenter

Model describing an NV center subject to a variable amount of decoherence. The dephasing rate encodes some useful information about the environment, which can be recovered by estimating the transverse relaxation time and the decaying exponent.

Constructor of the NVCenterDecoherence class.

Parameters

batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
params: List[Parameter]: List of unknown parameters to estimate in the NV center experiment, with their priors. It should contain the inverse of the characteristic time of the dephasing process, indicated with the symbol $T^{-1}$ and the exponent $\beta$ of the decay. This last parameter carries information on the spectral density of the noise.
prec{“float64”, “float32”}: Precision of the floating point operations in the simulation.
res: {“meas”, “time”}: Resource type for the present metrological task. It can be either the total evolution time, i.e. time, or the total number of measurements on the NV center, i.e. meas.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, meas_step: Tensor, num_systems: int = 1)

Model for the outcome of a photon counting measurement following a Ramsey sequence on the NV center sensor subject to dephasing noise. The probability of getting the outcome $+1$ is

(68) $p(+1|T, \beta, \tau) := \frac{1 + e^{-\left( \frac{\tau}{T}\right)^{ 20 \beta}}}{2} \; .$

The evolution time $\tau$ is controlled by the trainable agent and $T$ and $\beta$ are the two unknown characteristic parameters of the noise. The factor 20 appearing at the exponent is just the normalization factor we used for $\beta$ .

decoherence_estimation(args, batchsize: int, max_res: float, learning_rate: float = 0.001, gradient_accumulation: int = 1, cumulative_loss: bool = True, log_loss: bool = False, res: Literal['meas', 'time'] = 'meas', loss_normalization: bool = False, beta_nuisance: bool = False, fixed_beta: bool = False)

Simulates the Bayesian estimation of the decoherence parameters of a dephasing noise acting on an NV center. The control parameter is the free evolution time of the system during the Ramsey sequence. We have implement four strategies for the control of the evolution time:

Adaptive strategy with a trained neural network on the basis of the state of the particle filter (adaptive strategy).
Static strategy implemented with a neural network that receives in input the amount of already consumed resources (time or measurements)
Random strategy, with an evolution time chosen in the admissible interval for the values of $T^{-1}$ .
Inverse time strategy. The evolution time is is $\tau = \alpha_M^{\frac{1}{\widehat{\beta}}} \widehat{T^{-1}}$ for the measurement-limited estimation and $\tau = \alpha_T^{\frac{1}{\widehat{\beta}}} \widehat{T^{-1}}$ for the time-limited estimations, where $\alpha_M = 0.79681$ and $\alpha_M = 0.43711$ . These numerical coefficients come from the optimization of the Fisher information. For the simulations where $\beta$ is a nuisance parameter $\alpha_M$ is used also for the time-limited estimation.

This function trains the static and the adaptive strategies, and evaluates the error for all these four possibilities, in this order.

Achtung! In this example the static strategy is not implemented as a Tensor of controls for each individual measurement, like in the other examples. On the contrary it is implemented as a neural network that takes in input only the value of the consumed resources up to that point.

The measurement cycle is represented in the picture below.

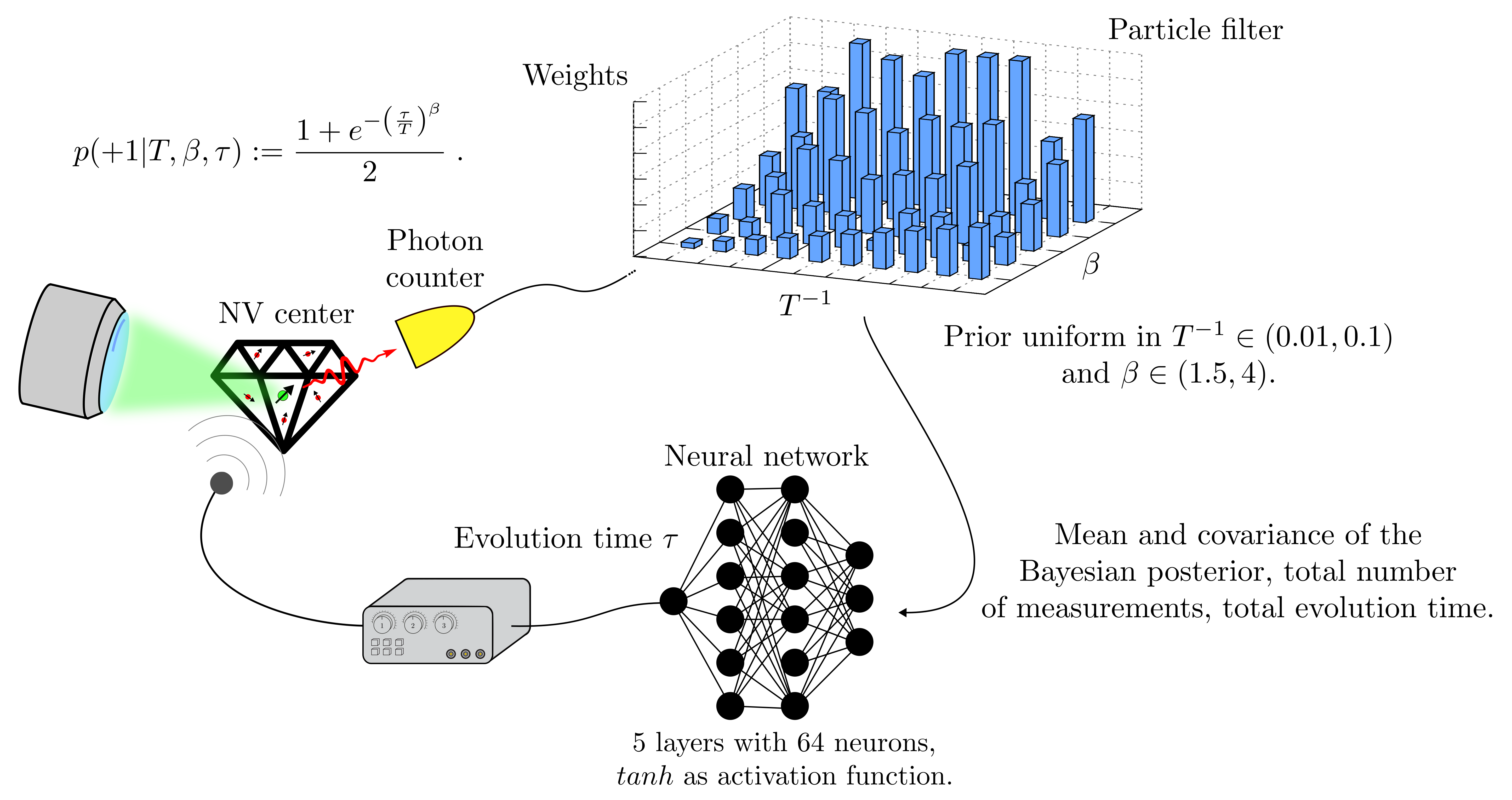
Parameters

args:: Arguments passed to the Python script.
batchsize: int: Batchsize of the simulation, i.e. number of estimations executed simultaneously.
max_res: float: Maximum amount of resources allowed to be consumed in the estimation.
learning_rate: float = 1e-3: Initial learning rate for the neural networks, for both the adaptive and static strategies. The learning rate decays with InverseSqrtDecay.
gradient_accumulation: int = 1: Flag of the train() function.
cumulative_loss: bool = False: Flag cumulative_loss.
log_loss: bool = False: Flag log_loss.
res: {“meas”, “time”}: Type of resource for the simulation. It can be either the number of measurements or the total evolution time.
loss_normalization: bool = False: Parameter loss_normalization passed to the constructor of the NVCenterDecoherence class.
beta_nuisance: bool = False: If this flag is True, the loss is computed only from the error on the inverse decay time $T^{-1}$ .
fixed_beta: bool = False: If this flag is True the decay exponent is set to $\beta=0.1$ .

main()

In this example we characterize the dephasing process of an NV center. We study three cases. In the first one the decaying exponent $\beta$ is unknown and it is treated as a nuisance parameter. Therefore, only the precision on the inverse decay time appears in the loss (the MSE). In the second case $\beta$ is known and fixed ( $20 \beta = 2$ ), and only $T^{-1}$ is estimated. In the third case both $\beta$ and $T^{-1}$ are unknown and are parameters of interest, but their MSE are not evenly weighted: the error $\Delta^2 \hat{\beta}$ weights half of $\Delta^2 \hat{T_2}^{-1}$ . This is done t equilibrate the different priors on the parameters and consider them on an equal footage.

The prior on $T^{-1}$ is uniform in (0.01, 0.1), and that of $\beta$ is uniform in (0.075, 0.2) (when it is not fixed), so that the interval for the actual exponent, which is $20 \beta$ (see model()) is (1.5, 4) 5.

In the following we report the estimator error (MSE) for a bounded number of measurement (on the left), and for a bounded total evolution time (on the right). These simulations are done by calling the function decoherence_estimation().

The adaptive and static strategies are compared with two simple choices for the controls. The first is a randomize strategy, according to which the inverse of the evolution time is randomly selected uniformly in (0.01, 0.1), while the second is a $\widehat{T^{-1}}$ strategy, according to which the inverse of the evolution time is chosen to be the current estimator for the inverse of the coherence time.

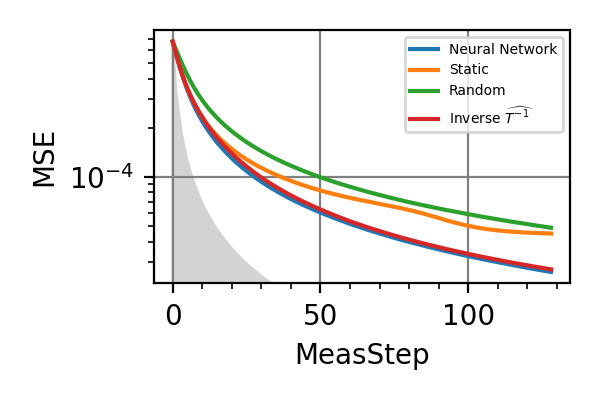
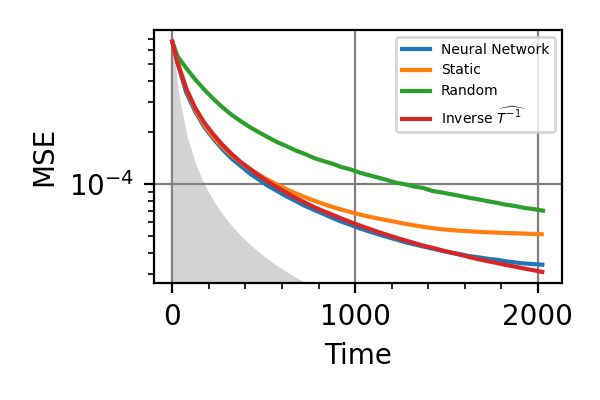
Fig. 29 Meas=128, beta nuisance	Fig. 30 Time=2048, beta nuisance
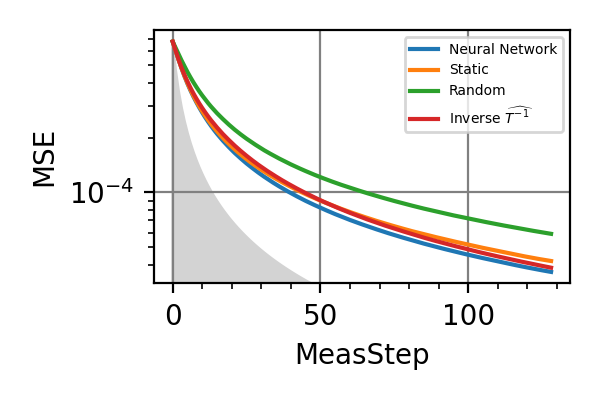
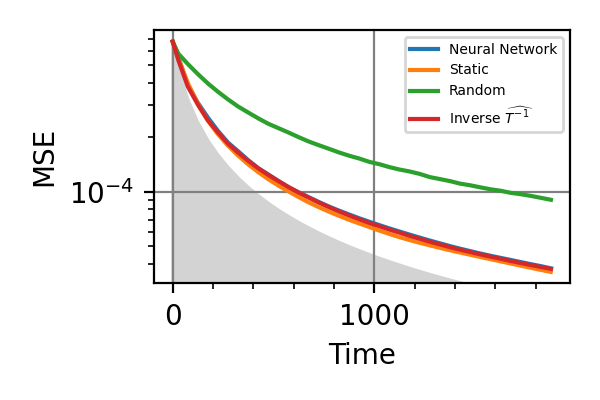
Fig. 31 Meas=128, fixed beta	Fig. 32 Time=2048, fixed beta
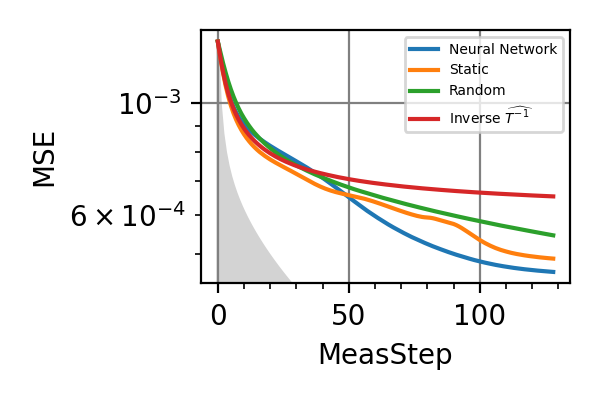
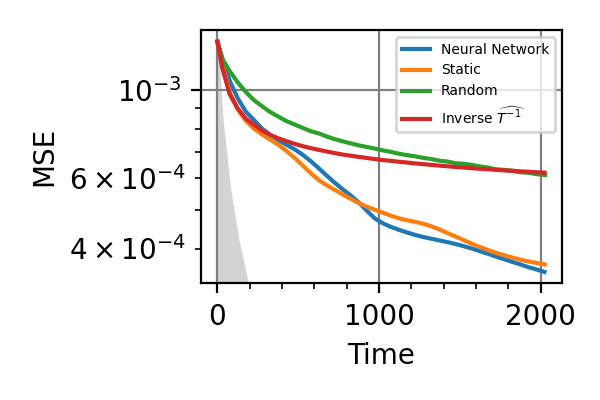
Fig. 33 Meas=128, both parameters	Fig. 34 Time=2048, both parameters

The shaded grey areas in the above plot indicate the Bayesian Cramér-Rao bound, which is the the ultimate precision bound computed from the Fisher information.

There is no advantage in using a NN instead of the strategies that optimize the Fisher information.

Notes

Some application of the estimation of the decoherence time involve the measure of the radical concentration in a biological sample and the measurement of the local conductivity through the Johnson noise.

All the training of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

5(1,2): https://arxiv.org/pdf/2210.06103.pdf

parse_args()

Arguments

scratch_dir: str, required: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./nv_center_decoherence/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./nv_center_decoherence/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float32”: Floating point precision of the whole simulation.
n: int = 64: Number of neurons per layer in the neural network.
num_particles: int = 2048: Number of particles in the ensemble representing the posterior.
iterations: int = 4096: Number of training steps.
scatter_points: int = 32: Number of points in the Resources/Precision csv produced by performance_evaluation().

Dolinar (Dolan) receiver

class AgnosticDolinar(batchsize: int, params: List[Parameter], n: int, resources: str = 'alpha', prec: str = 'float64')

Bases: StatefulPhysicalModel

Schematization of the agnostic Dolinar receiver 6.

The task is to discriminate between $|+\alpha\rangle$ and $|-\alpha\rangle$ , given a single copy of $| \pm \alpha\rangle$ and $n$ copies of $|\alpha\rangle$ , that have been prepared in another lab. At difference with the usual Dolinar receiver the intensity of the signal $\alpha$ is not known, but can be estimated from $|\alpha\rangle^{\otimes n}$ to adapt the strategy. The physical motivations behind this model is that of a series of wires, with only one carrying the signal, subject to a loss noise of fluctuating intensity.

6: F. Zoratti, N. Dalla Pozza, M. Fanizza, and V. Giovannetti, Phys. Rev. A 104, 042606 (2021).

Constructor of the AgnosticDolinar class.

Parameters

batchsize: int

Number of agnostic Dolinar receivers simulated at the same time in a mini-batch.

params: List[Parameter]

List of parameters. It must contain the continuous parameter alpha with its admissible range of values, and the discrete sign parameter, that can take the values (-1, +1).

n: int

Number of states $|\alpha \rangle$ that the agnostic Dolinar receiver consumes to make a decision on the sign of the sign of the signal.

Achtung! Note that in the simulation n+1 measurement are actually performed, because both outputs of the last beam splitter are measured.

resources: {“alpha”, “step”}

Resources of the model, can be the amplitude $\alpha$ of the signal or the number of state $|\alpha\rangle$ consumed in the procedure.

prec: str = “float64”

Floating point precision of the model.

count_resources(resources: Tensor, controls: Tensor, true_values: Tensor, meas_step: Tensor) → Tensor: The resources can be either the number of states $|\alpha\rangle$ consumed, which is update after every beam splitter, or the amplitude $\alpha$ , that is related to the mean number of photons in the signal.

initialize_state(parameters: Tensor, num_systems: int) → Tensor: State initialization for the agnostic Dolinar receiver. The state contains the amplitude of the remaining signal after the measurements (for both hypothesis) and the total number of measured photons.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, state: Tensor, meas_step: Tensor, num_systems: int = 1): Probability of observing the number of photons outcomes in a photon counter measurement in the agnostic Dolinar receiver.

perform_measurement(controls: Tensor, parameters: Tensor, true_state: Tensor, meas_step: Tensor, rangen: Generator): The signal $| \pm \alpha\rangle$ and the reference states $\alpha$ are sequentially mixed on a beam splitter with tunable transmission $\theta$ , and one output of the beam splitter is measured through photon counting, while the other gets mixed again. The left over signal after n uses of the beam splitter is then measured on a photon counter.

class DolinarSimulation(particle_filter: ParticleFilter, phys_model: AgnosticDolinar, control_strategy: Callable, simpars: SimulationParameters, loss: int = 3)

Bases: StatefulSimulation

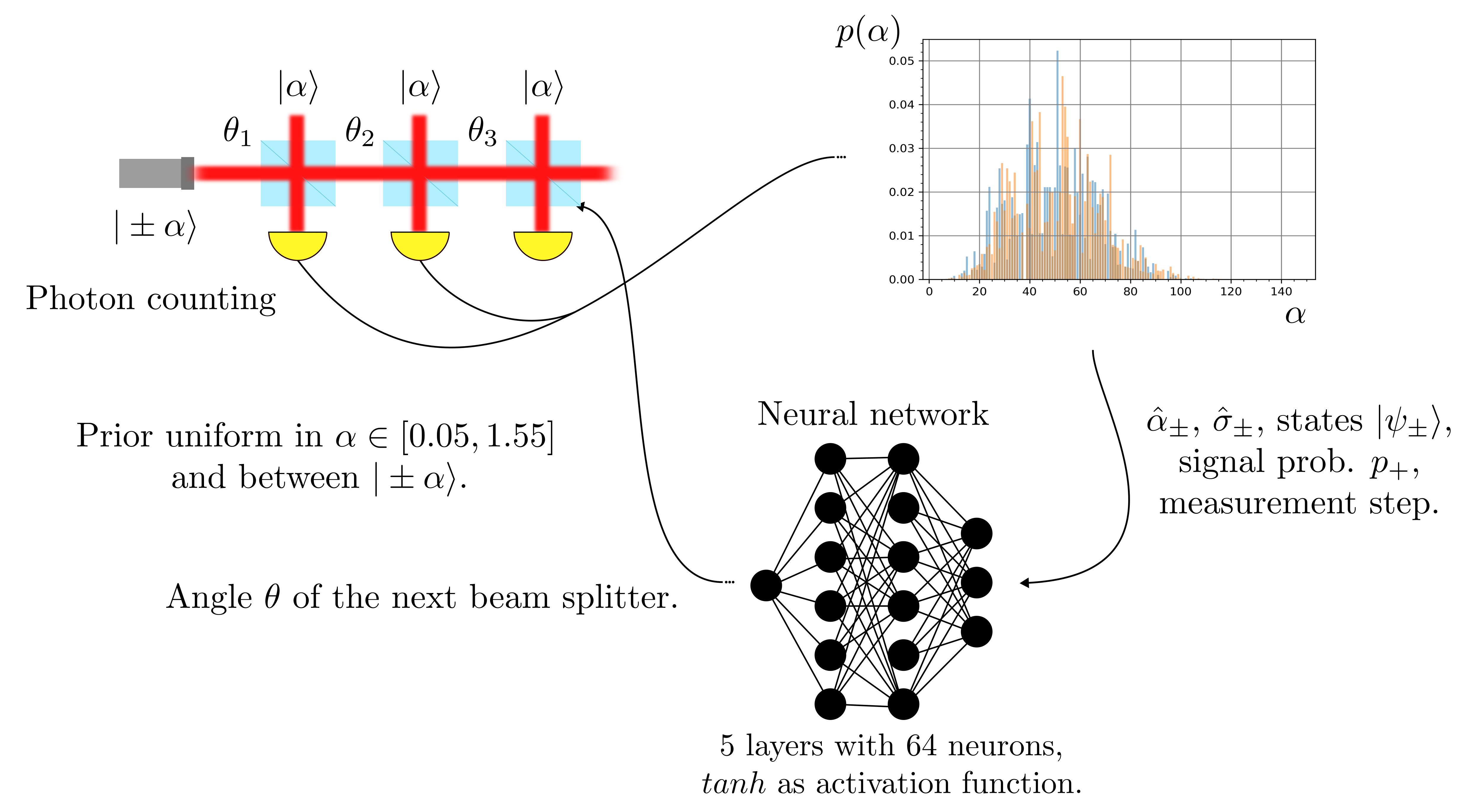
Simulation class for the agnostic Dolinar receiver. It works with a ParticleFilter and a AgnosticDolinar objects.

The measurement loop is showed in the following picture.

Constructor of the DolinarSimulation class.

Parameters

particle_filter: ParticleFilter: Particle filter responsible for the update of the Bayesian posterior on $\alpha$ and on the sign of the signal. It contains the methods for applying the Bayes rule and computing Bayesian estimators from the posterior.
phys_model: AgnosticDolinar: Model of the agnostic Dolinar receiver.
simpars: SimulationParameters: Parameter simpars passed to the class constructor.
loss: int = 3: Type of loss to be used in the simulation. It regulates the behavior of the loss_function() method. There are nine possible losses to choose from. These are explained in the documentation of loss_function().

generate_input(weights: Tensor, particles: Tensor, state_ensemble: Tensor, meas_step: Tensor, used_resources: Tensor, rangen: Generator)

This method collects the information on $\alpha$ and on the sign of the signal produced by the particle filter and builds from them the input_strategy object to be fed to the neural network. This Tensor has nine scalar components, that are:

$\psi_{+}$ , the normalized intensity of the signal after the measurements, assuming that it was $|+\alpha\rangle$ at the beginning.
$\hat{\alpha}_+$ , the mean posterior estimator for signal intensity assuming $|+\alpha\rangle$ .
$\hat{\sigma}_+$ , the variance of the posterior distribution for the signal intensity, assuming $|+\alpha\rangle$ .
$\psi_{-}$ , the normalized intensity of the signal after the measurements, assuming that it was $|-\alpha\rangle$ at the beginning.
$\hat{\alpha}_{-}$ , the mean posterior estimator for signal intensity assuming $|-\alpha\rangle$ .
$\hat{\sigma}_-$ , the variance of the posterior distribution for the signal intensity, assuming $|-\alpha\rangle$ .
$\hat{p}_{+}$ the posterior probability for the original signal to be $|+\alpha\rangle$ ,
the index of the current measurement meas_step normalized against the total number of measurements,
the total number of photons measured, up to the point this method is called.

loss_function(weights: Tensor, particles: Tensor, true_state: Tensor, state_ensemble: Tensor, true_values: Tensor, used_resources: Tensor, meas_step: Tensor)

The loss of the agnostic Dolinar receiver measures the error in guessing the sign of the signal $|\pm \alpha \rangle$ , after the signal has been completely measured.

There are nine possible choices for the loss, which can be tuned through the parameter loss passed to the constructor of the DolinarSimulation class. Before analyzing one by one these losses we establish some notation. $\hat{p}_{+}$ is the posterior probability that the original signal is $| + \alpha \rangle$ , $\hat{p}_{-} = 1 -\hat{p}_{+}$ , $s$ is the sign of the signal in $| s \alpha \rangle$ , and $n_{\text{Phot}}$ is the total number of observed photons. The error probability given by the resource limited Helstrom bound is indicated with $p_H(\alpha)$ . This is computed by the function helstrom_bound(). We also define the Kronecker delta function

(69) $\delta (x, y) = \begin{cases} 1 \quad \text{if} \quad x=y \; , \\ 0 \quad \text{if} \quad x \neq y \; . \end{cases}$

There are two possible policies for guessing the signal sign, that we indicate respectively with $G_{\text{Bayes}}$ and $G_{\text{Parity}}$ . They are respectively

(70) $G_{\text{Bayes}} (\hat{p}_{+}) = \begin{cases} +1 \quad \text{if} \quad \hat{p}_{+} > 0.5 \; ,\\ -1 \quad \text{if} \quad \hat{p}_{+} \le 0.5 \; ,\\ \end{cases}$

and

(71) $G_{\text{Parity}} (n_{\text{Phot}})= \begin{cases} +1 \quad \text{if} \quad n_{\text{Phot}} \bmod 2 = 0 \; ,\\ -1 \quad \text{if} \quad n_{\text{Phot}} \bmod 2 = 1 \; .\\ \end{cases}$

The possible choices for the loss are

loss=0: $\ell (\hat{p}_{+}, s) = 1-\delta(G_{\text{Bayes}}, s)$ ,
loss=1: $\ell (\hat{p}_{+}, s) = 1-\hat{p}_{s}$ ,
loss=2: $\ell (n_{\text{Phot}}, s) = 1-\delta(G_{\text{Parity}}, s)$ ,
loss=3: $\ell (\hat{p}_{+}, s, \alpha) = 1-\delta(G_{\text{Bayes}}, s) - p_H(\alpha)$ ,
loss=4: $\ell (\hat{p}_{+}, s, \alpha) = 1-\hat{p}_{s} - p_H(\alpha)$ ,
loss=5: $\ell (n_{\text{Phot}}, s, \alpha) = 1-\delta(G_{\text{Parity}}, s) - p_H(\alpha)$ ,
loss=6: $\ell (\hat{p}_{+}, s, \alpha) = \frac{1-\delta(G_{\text{Bayes}}, s)}{p_H(\alpha)}$ ,
loss=7: $\ell (\hat{p}_{+}, s, \alpha) = \frac{1-\hat{p}_{s}}{p_H(\alpha)}$ ,
loss=8: $\ell (n_{\text{Phot}}, s, \alpha) = \frac{1-\delta(G_{\text{Parity}}, s)}{p_H(\alpha)}$ ,

Notes

The optimization with loss=3 works better for small $\alpha$ then for large $\alpha$ . This is because the scalar loss is the mean of the error probability on the batch and it is not so relevant to optimize the estimations those regions of the parameter $\alpha$ that have low error probability anyway. To summarize, loss=3 makes the optimization concentrate on the region of small $\alpha$ , since this region dominates the error.

Achtung!: A constant added to the loss is not irrelevant for the training, since the loss itself and not only the gradient is appears in the gradient descent update.

dolinar_receiver(args, num_steps: int, loss: int = 3, learning_rate: float = 0.01)

Training and performance evaluation of the neural network and the static strategies that control the beam splitter reflectivity in the agnostic Dolinar receiver.

Parameters

args:: Arguments passed to the Python script.
num_steps: int: Number of reference states $\alpha$ in the Dolinar receiver.
loss: int = 3: Type of loss used for the training, among the ones described in the documentation of loss_function(). The loss used for the performances evaluation is always loss=0.
learning_rate: float = 1e-2: Initial learning rate for the neural network. The initial learning rate of the static strategy is fixed to 1e-2. They both decay with InverseSqrtDecay.

helstrom_bound(batchsize: int, n: int, alpha: Tensor, iterations: int = 200, prec: str = 'float64')

Calculates the Helstrom bound for the agnostic Dolinar receiver with n copies of $|\alpha\rangle$ . It is the lower bound on the error probability for the discrimination task and it is given by the formula

(72) $p_H(\alpha) := \frac{1}{2} \left( 1- \frac{1}{2} \sum_{k=0}^\infty \mathfrak{p} (k; \sqrt{n+1}\alpha) \sqrt{1-\left( \frac{n-1}{n+1} \right)^{2 k}} \right) \; ,$

where $\mathfrak{p} (k; \mu)$ is the probability distribution of a Poissonian variable, i.e.

(73) $\mathfrak{p} (k; \mu) := \frac{\mu^k e^{-\mu}}{k!} \; .$

Parameters

batchsize: int: Number of bounds to be computed simultaneously, it is the first dimension of the alpha Tensor.
n: int: Number of copies of $|\alpha\rangle$ at disposal.
alpha: Tensor: Tensor of shape (batchsize, 1), with the amplitudes of the coherent states for each discrimination task.
iterations: int = 200: There is no closed formula for the error probability, this parameter is the number of summand to be computed in Eq.72.
prec: str = “float64”: Floating point precision of the alpha parameter.

Returns

Tensor:: Tensor of shape (batchsize, 1) and type prec containing the evaluated values of the Helstrom error probability for the discrimination taks.

main()

We have trained the optimal adaptive and static strategies for the agnostic Dolinar receiver.

The error probabilities as a function of $\alpha$ are reported in the following figure for $n=4$ and $n=8$ reference states $|\alpha\rangle$ , for two different training losses (loss=3 and loss=6).

The Heterodyne and Photon counting are two 2-stage adaptive strategies based on first measuring all the reference state $|\alpha\rangle^{\otimes n}$ and then trying to discriminate the signal based on the acquired information 5.

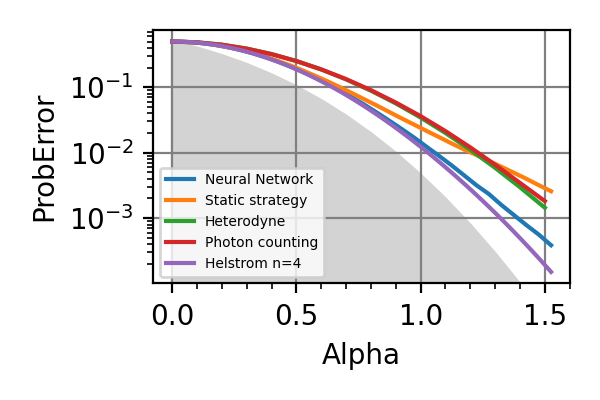
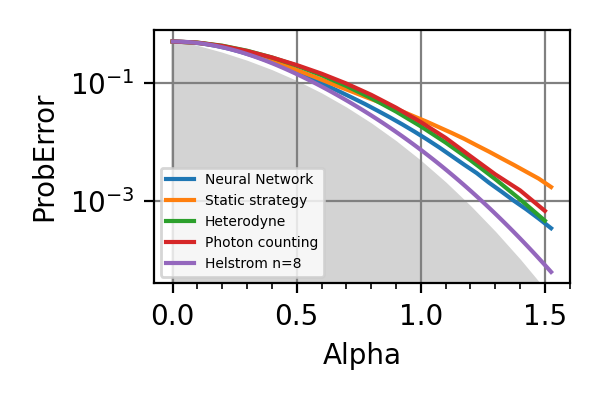
Fig. 35 n=4, loss=3	Fig. 36 n=8, loss=3
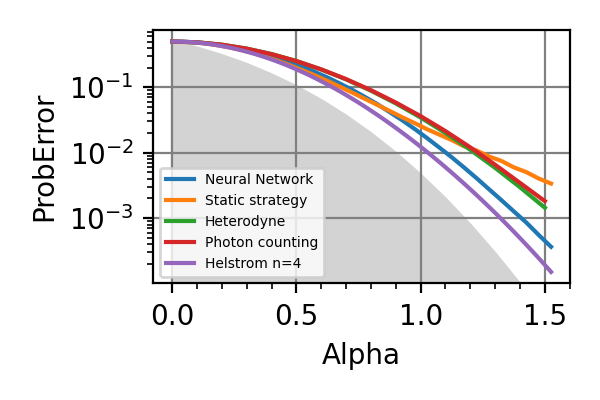
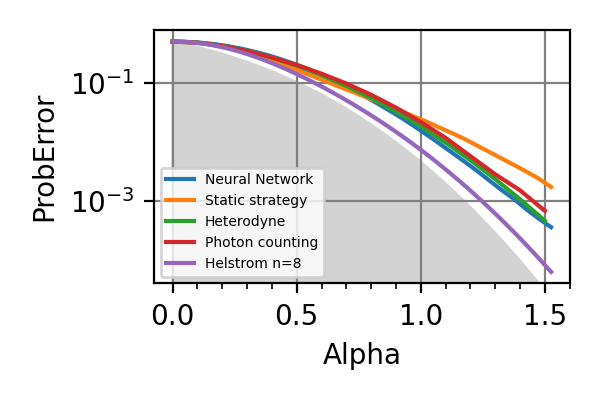
Fig. 37 n=4, loss=6	Fig. 38 n=8, loss=6

The shaded grey areas in the above plot indicate the Helstrom bound for the discrimination of $|\pm \alpha \rangle$ .

The loss=3 seems to be uniformly superior to loss=6 for every value of $\alpha$ . The advantage of using the neural network strategy is very contained with respect to already known strategies for $n=8$ but it is significant for $n=4$ . Instead of a NN a decision tree could have also been a viable strategy for controlling the beam splitters as done in the module dolinar_three. As expected the gap between the precision of the adaptive and of the non-adaptive strategies increases with the number of photons in the signal.

Notes

The loss used in calling performance_evaluation() is always loss=0.

The resources used in calling store_input_control() are always the number of measurements.

An application of machine learning (decision trees) to the Dolinar receiver have been presented also by Cui et al 7.

Known bugs: the training on the GPU freezes if the parameter alpha_bound is set to be too large. This is probably due to a bug in the implementation of the function random.poisson. A preliminary work-around has shown that reimplementing the extraction from a Poissonian distribution with random.categorical would solve the problem.

All the training of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

7: C. Cui, W. Horrocks, S. Hao et al., Light Sci Appl. 11, 344 (2022).

parse_args()

Arguments

scratch_dir: str: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./dolinar/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./dolinar/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float64”: Floating point precision of the whole simulation.
batchsize: int = 4096: Batchsize of the simulation.
n: int = 64: Number of neurons per layer in the neural network.
num_particles: int = 512: Number of particles in the ensemble representing the posterior.
num_steps: int = 8: Number of reference states $|\alpha\rangle$ , i.e. number of beam splitters.
training_loss: int = 3: Loss used in the training. It is an integer in th range [0, 8]. The various possible losses are reported in the description of the loss_function() method.
iterations: int = 32768: Number of training steps.

Quantum ML classifier

class CoherentStates(batchsize: int, prec: str = 'float64')

Bases: object

This class contains the methods to operated on one ore more bosonic wires carrying coherent states. It can’t deal with squeezing or with noise, only with displacements, phase shifts and photon counting measurements.

Notes

The covariance matrix of the system is always proportional to the identity and corresponds to zero temperature.

Constructor of the CoherentStates class.

Parameters

batchsize: int

Number of experiments that are simultaneously treated by the object.

Achtung! This is not the number of bosonic lines that an object of this class can deal with. This is in fact not an attribute of the class, and is not fixed during the initialization.

apply_bs_network(variables_real: Tensor, variables_imag: Tensor, input_channels: Tensor, num_wires: int)

Applies the beam splitter network identified by variables_real and variables_imag to the state carried by the bosonic lines.

Parameters

variables_real: Tensor: Tensor of shape (batchsize, ?, num_wires, num_wires) and type prec.
variables_imag: Tensor: Tensor of shape (batchsize, ?, num_wires, num_wires) and type prec.
input_channels: Tensor: Displacement vector of the bosonic wires. It is a Tensor of type prec and shape (batchsize, ?, 2 num_wires). The components of the i-th wire are at position i and i+num_wires.
num_wires: int: Number of wires in the system.

Returns

Tensor: Tensor of shape (batchsize, ?, 2 num_wires) and type prec, containing the evolved displacements of the bosonic wires state.

apply_bs_network_from_unitary(unitary: Tensor, input_channels: Tensor)

Applies the beam splitter identified by variables_real and variables_imag.

Parameters

unitary: Tensor: Tensor of shape (batchsize, ?, num_wires, num_wires) and type complex64 if prec is float32 or complex128 if prec if float64.
input_channels: Tensor: Displacement vector of the bosonic wires. It is a Tensor of type prec and shape (batchsize, ?, 2 num_wires). The components of the i-th wire are at position i and i+num_wires.

Returns

Tensor: Tensor of shape (batchsize, ?, 2 num_wires) and type prec, containing the evolved displacements of the bosonic wires wires.

Notes

The covariance matrix of the system is always proportional to the identity and corresponds to zero temperature.

beamsplitter(input1: Tensor, input2: Tensor, theta: Tensor, phi: Tensor) → Tuple[Tensor, Tensor]

Beam splitter (BS) operating on two bosonic modes carrying coherent states. It returns the two states outputted by the BS.

Parameters

input1: Tensor: Tensor of shape (bs, ?, 2) and of type prec containing the x and y components of the first incident state on the BS.
input2: Tensor: Tensor of shape (bs, ?, 2) and of type prec containing the x and y components of the second incident state on the BS.
theta: Tensor: Tensor of shape (bs, ?) and of type prec. It contains the transmission coefficient of the BS. It is indicated with $\theta$ in the formulas.
phi:: Tensor of shape (bs, ?) and of type prec. It contains the phase applied by the BS. It is indicated with $\phi$ in the formulas.

Returns

Tensor:: Tensor of shape (bs, ?, 2) and type prec. Contains the first output state of the BS.
Tensor:: Tensor of shape (bs, ?, 2) and type prec. Contains the second output state of the BS.

mean_phot(input_state: Tensor) → Tensor

Returns the mean photon number on a coherent state.

Parameters

input_state: Tensor: Tensor of shape (bs, ?, 2) and of type prec containing the x and y components of the coherent state.

Returns

Tensor: Tensor of shape (bs, ?) and type prec containing the average number of photons of the coherent states described in input_state.

phase_shift(input_state: Tensor, phase: Tensor) → Tensor

Applies a phase shift on the coherent states encoded in input_state.

Parameters

input_state: Tensor: Tensor of shape (bs, ?, 2) and of type prec containing the x and y components of the coherent state to be rotated.
phase: Tensor: Tensor of shape (bs, ?) containing the phase for the rotation of each state in the batch.

Returns

Tensor:: Tensor of shape (bs, ?, 2) and of type prec containing the rotated coherent state.

photon_counter(input_state: Tensor, rangen: Generator, num_systems: int = 1) → Tuple[Tensor, Tensor]

Photon counting measurement on a bosonic line carrying a coherent state.

Parameters

input_state: Tensor: Tensor of shape (bs, ?, 2) and of type prec containing the x and y components of the coherent state on which the photon counting measurement will be performed.
rangen: Generator: Random number generator from the module tensorflow.random.
num_systems: int = 1: Number of independent coherent states processed per batch. It is the size of the second dimension of input_state.

Returns

outcomes: Tensor: Tensor of shape (bs, num_systems, 1) and type prec containing the outcomes of the photon counting measurement (the number of photons).
log_prob: Tensor: Tensor of shape (bs, num_systems) and type prec containing the logarithm of the probability of the observed number of photons.

postselect_photon_counter(input_state: Tensor, outcomes: Tensor) → Tensor

Returns the logarithm of the probability of observing outcomes after a photon counting measurement on input_state.

Parameters

input_state: Tensor: Tensor of shape (bs, ?, 2) and of type prec containing the x and y components of the coherent state on which the photon counting measurement is performed.
outcomes: Tensor: Tensor of shape (bs, ?, 1) and type prec containing the outcomes of the photon counting measurement (the number of photons).

Returns

log_prob: Tensor: Tensor of shape (bs, ?) and type prec containing the logarithm of the probability of observing outcomes on input_state.

class QMLDiscriminator(batchsize: int, params: List[Parameter], num_ref: int, resources: str = 'alpha', arch: str = 'serial', decision_tree: bool = False, prec: str = 'float64')

Bases: StatefulPhysicalModel, CoherentStates

Blueprint class for the quantum Machine Learning (QML) based classifier able to distinguish between three coherent states $|\alpha_0\rangle$ , $|\alpha_1\rangle$ , $|\alpha_2\rangle$ , given $n$ copies of each of them, which constitute the quantum training set. The signal state is a single copy of a coherent state, promised to be one of the three training states, i.e. $|\alpha_s\rangle$ with s=0, 1, 2.

Notes

The priors on the real components of the training states $|\alpha_0\rangle$ , $|\alpha_1\rangle$ , $|\alpha_2\rangle$ are uniform, as the prior on the signal classes s=0, 1, 2.

Attributes

bs: int: The batchsize of the physical model, i.e., the number of simultaneous signal testings simulated.
controls: List[Control]: The controls of the QML classifier are the transmission coefficient and the extra phase of the beam splitter that precedes the photon counting. These can be chosen adaptively according to the previous measurements outcomes.
params: List[Parameter]: List of parameters to be estimated, passed to the class constructor. These are the real components of the unknown training states (continuous parameter), and the class of the signal.
controls_size: int = 2: Number of scalar controls in the QML classifier, i.e. 2, the two angles $\theta$ and $\phi$ characterizing the beam splitter transformation performed by beamsplitter().
d: int = 7: The number of unknown parameters to estimate, i.e. 7.
state_specifics: StateSpecifics: Size of the state of the apparatus, which can be 2 for the serial architecture or 6 for the parallel, plus the type of the state, i.e. prec. If decision_tree=True the size of the state is increased by one.
recompute_state: bool = True: Flag to the constructor of the PhysicalModel class.
outcomes_size: int = 1: Number of scalar outcomes for each measurement in the apparatus, i.e. one, the number of photons in the photon counter.
prec: str: The floating point precision of the controls, outcomes, and parameters.
num_ref: int: Number of copies of each training state, passed to the class constructor.
num_steps: int: Total number of photon counting measurements in the apparatus. It depends on num_ref and on the architecture, in particular it is 3 num_ref+1 for the serial apparatus and 3 num_ref+3 for the parallel one.
resources: {“alpha”, “step”}: Resource type passes to the class constructor. It can be the average number of photons in the device (“alpha”) or the number of measurements (“step”).
dt: bool: Flag decision_tree passed to the class constructor. It should be activated if a decision tree is used for controlling the beam splitters.
arch: {“serial”, “parallel”}: Architecture of the QML classifier passed to the class constructor. An object of the child class QMLDiscriminatorSerial will have arch=”serial”, while an instance of QMLDiscriminatorParallel will have arch=”parallel”.

Constructor of the QMLDiscriminator class.

Parameters

batchsize: int

Batchsize of the physical model, i.e., the number of simultaneous estimations.

params: List[Parameter]

A list of unknown parameters to be estimated, alongside the corresponding sets of admissible values. For the three states Dolinar these are the x and y components of $|\alpha_0\rangle$ , $|\alpha_1\rangle$ , $|\alpha_2\rangle$ (six continuous parameters in total) plus the class of the signal, which is a discrete parameter that takes values in the set {0, 1, 2}.

num_ref: int

Number of copies of each training state.

resources: {“alpha”, “step”}

Two types of resource counting are possible in the apparatus. The first is the the total number of photon counting measurements, corresponding to the value “step” for the resources parameter. The second is the mean number of photons in the apparatus, corresponding to the value “alpha” for this parameter. The average photon number is

where $n$ is the number of training copies, i.e. num_ref.

arch: {“serial”, “parallel”}

Architecture of the QML classifier.

decision_tree: bool = False

If this flag is True, then the physical model of the device is set up to be used with a decision tree controlling the beam splitters. This affect the state size, which now contains an integer that univocally identifies the string of outcomes that have already appeared in the photon counting measurements.

prec: str = “float64”

Floating point precision of the controls, outcomes, and parameters.

count_resources(resources: Tensor, controls: Tensor, true_values: Tensor, meas_step: Tensor) → Tensor: The resources can be either the number of measurement steps or the mean number of photons in the system. In the second case the resource is considered consumed after the last photon counting measurement closing the device.

class QMLDiscriminatorParallel(batchsize: int, params: List[Parameter], num_ref: int, resources: str = 'alpha', decision_tree: bool = False, prec: str = 'float64')

Bases: QMLDiscriminator

Parallel strategy for classifying a coherent state, given three hypothesis.

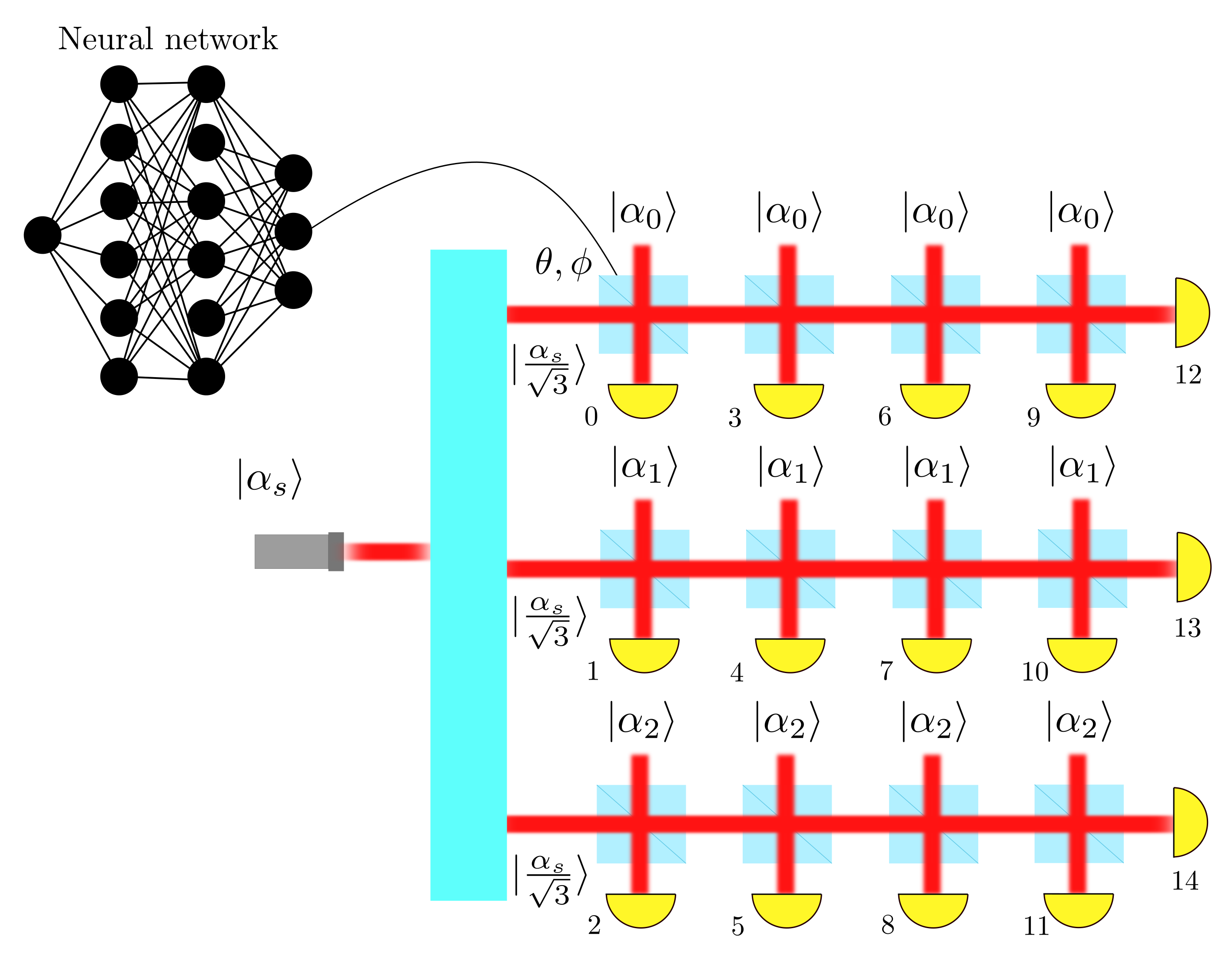
The original signal is first equally splitted on three wires, i.e. $|\alpha_s\rangle \rightarrow |\frac{\alpha_s}{\sqrt{3}}\rangle^{\otimes 3}$ . On each line the signal is mixed with the copies of the same training state.

The order of the measurements is show in the figure near the symbol for the photon counter. The measurements are not really done in parallel as it can be seen. All the outcomes of the previous photon counters contributes to the determination of the next controls through the particle filter and the neural network (or the decision tree). In order to realize the measurements in this order the optical path along the the wires should be prolonged differently.

Constructor of the QMLDiscriminatorParallel class.

Parameters

batchsize: int: Number of simultaneous estimations.
params: List[Parameter]: Contains the real components of the unknown training states and the signal to be classified.
num_ref: int: Number of training states for each class.
resources: {“alpha”, “step”}: Type of resources counted.
decision_tree: bool = False: Indicates that a decision tree is used for controlling the beam splitters.
prec:: Floating point precision of the estimation.

initialize_state(parameters: Tensor, num_systems: int) → Tensor

Initializes the true state of the signal $|\frac{\alpha_s}{\sqrt{3}}\rangle^{\otimes 3}$ for the parallel device.

Parameters

parameters: Tensor: Tensor of shape (bs, num_system, 7) and type prec containing the real components of the three training states and the index classifying the true signal (the seventh parameter).
num_systems: int: Size of the second dimension of the parameters Tensor. It is the number of systems treated per batch element.

Returns

Tensor:: Tensor of shape (bs, num_system, 6) containing the state of the true signal, equally distributed on the three lines of the discrimination device with parallel architecture. If decision_tree=True the size of the last dimension of the returned Tensor is 7.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, state: Tensor, meas_step: Tensor, num_systems: int = 1)

Probability of observing a certain number of photons in a photon counting measurement in the parallel device.

Parameters

outcomes:: Tensor of shape (bs, num_systems, 1) and type prec containing the observed number of photons in a measurement.
controls: Tensor: Tensor of shape (bs, num_systems, 2) and of type prec containing the two angles $\theta$ and $\phi$ characterizing the BS placed before a photon counter.
parameters: Tensor: Tensor of shape (bs, num_systems, 7) and type prec containing the six real components of the three training states plus the signal class.
state: Tensor: Tensor of shape (bs, num_systems, 6) containing the real components in the phase space of the signal traveling through the three wires of the apparatus. If decision_tree=True the shape of this Tensor is (bs, num_systems, 7) and it contains also the whole history of outcomes codified in the last entry.
meas_step: Tensor: Tensor of shape (bs, num_systems, 1) and type prec. It is the index of the current measurement and starts from zero.
num_systems: int = 1: Number of system treated for each element of the batch.

Return

log_prob: Tensor: Tensor of shape (bs, num_systems) and type prec containing the logarithm of the probability of getting the observed number of photons.
state: Tensor: Tensor of shape (bs, num_systems, 6) and type prec with the state of the signal evolved after the photon counting measurement. If decision_tree=True the shape of this Tensor is (bs, num_systems, 7) and it contains also the whole history of outcomes codified in the last entry.

perform_measurement(controls: Tensor, parameters: Tensor, true_state: Tensor, meas_step: Tensor, rangen: Tensor)

Mixing of the signal on one wire with the corresponding training state and photon counting on one end of the beam splitter.

Parameters

controls: Tensor: Tensor of shape (bs, 1, 2) and of type prec containing the two angles $\theta$ and $\phi$ characterizing the BS placed before a photon counter.
parameters: Tensor: Tensor of shape (bs, 1, 7) and type prec containing the six real components of the three training states plus the signal class.
true_state: Tensor: Tensor of shape (bs, 1, 6) containing the real components in the phase space of the signal traveling through the three wires of the apparatus. If decision_tree=True the shape of this Tensor is (bs, 1, 7) and it contains also the whole history of outcomes codified in the last entry.
meas_step: Tensor: Tensor of shape (bs, 1, 1) and type prec. It is the index of the current measurement and starts from zero.

Return

outcomes: Tensor: Tensor of shape (bs, 1, 1) and type prec containing the number of photons observed in the photon counting measurement.
log_prob: Tensor: Tensor of shape (bs, 1) and type prec containing the logarithm of the probability of getting the observed number of photons.
state: Tensor: Tensor of shape (bs, 1, 6) and type prec with the state of the signal evolved after the photon counting measurement. If decision_tree=True the shape of this Tensor is (bs, 1, 7) and it contains also the whole history of outcomes codified in the last entry.

class QMLDiscriminatorSerial(batchsize: int, params: List[Parameter], num_ref: int, resources: str = 'alpha', prec: str = 'float64', decision_tree: bool = False)

Bases: QMLDiscriminator

Serial strategy for classifying a coherent state, given three hypothesis.

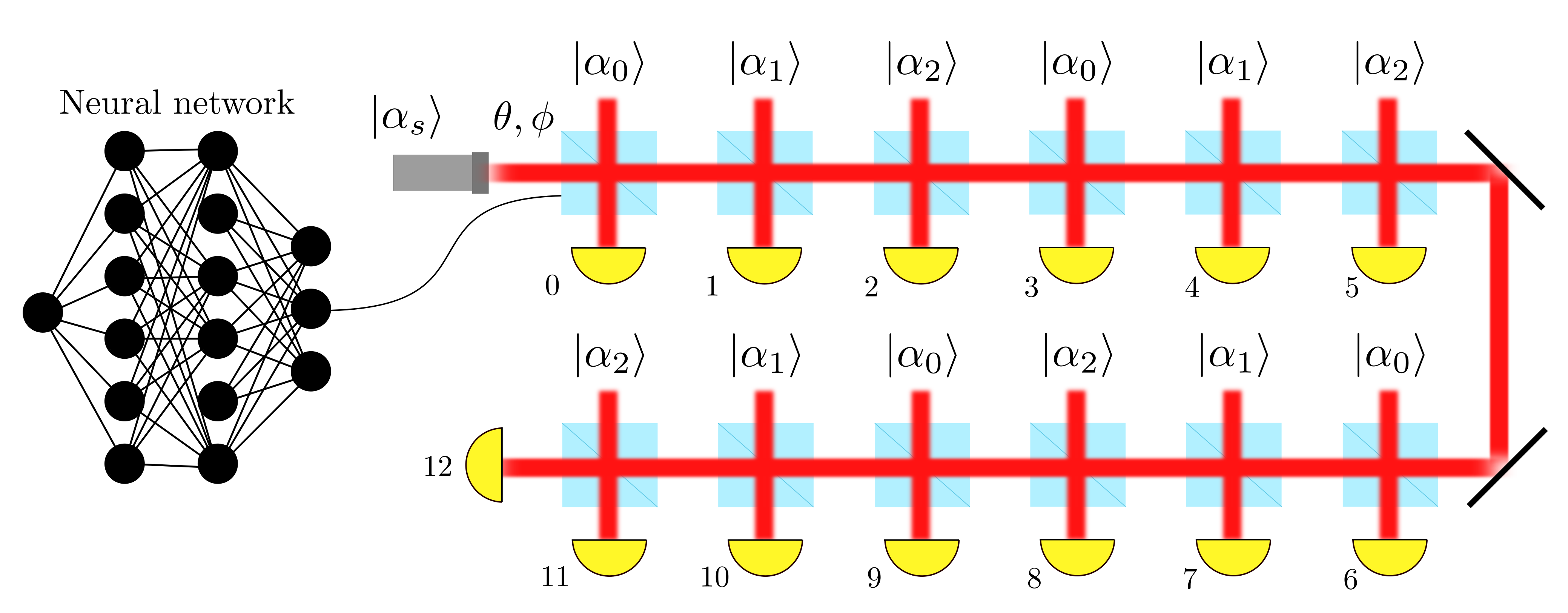
The signal $|\alpha_s\rangle$ is alternatively mixed with the training states and measured.

The order of the measurements is shown in the figure near the symbols for the for the photon counters. All the outcomes of the previous photon counters contribute to the determination of the next controls through the particle filter and the neural network (or the decision tree)

Constructor of the QMLDiscriminatorSerial class.

Parameters

batchsize: int: Number of simultaneous estimations.
params:: Real components of the unknown training states and signal to be classified.
num_ref: int: Number of training states for each class.
resources: {“alpha”, “step”}: Type of resources counted.
prec:: Floating point precision of the estimation.

initialize_state(parameters: Tensor, num_systems: int) → Tensor

Initializes the true state of the signal $|\alpha_s\rangle$ for the serial architecture.

Parameters

parameters: Tensor[bs, num_systems, 7]: Tensor of shape (bs, num_system, 7) and type prec containing the real components of the three training states and the index classifying the true signal (the seventh parameter).
num_systems: int: Size of the second dimension of the parameters tensor. It is the number of systems treated per batch element.

Returns

Tensor:: Tensor of shape (bs, num_system, 2) containing the initial state of the signal $|\alpha_s\rangle$ , computed according to parameters. If decision_tree=True the size of the last dimension of the returned Tensor is 3.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, state: Tensor, meas_step: Tensor, num_systems: int = 1) → Tuple[Tensor, Tensor]

Probability of observing a certain number of photons in a photon counting measurement in the serial device.

Parameters

outcomes:: Tensor of shape (bs, num_systems, 1) and type prec containing the observed number of photons in a measurement.
controls: Tensor: Tensor of shape (bs, num_systems, 2) and of type prec containing the two angles $\theta$ and $\phi$ characterizing the BS placed before a photon counter.
parameters: Tensor: Tensor of shape (bs, num_systems, 7) and type prec containing the six real components of the three training states plus the signal class.
state: Tensor: Tensor of shape (bs, num_systems, 2) containing the real components in the phase space of the signal traveling through the apparatus. If decision_tree=True the shape of this Tensor is (bs, num_systems, 3) and it contains also the whole history of outcomes codified in the last entry.
meas_step: Tensor: Tensor of shape (bs, num_systems, 1) and type prec. It is the index of the current measurement and starts from zero.
num_systems: int = 1: Number of system treated for each element of the batch.

Return

log_prob: Tensor: Tensor of shape (bs, num_systems) and type prec containing the logarithm of the probability of getting the observed number of photons.
state: Tensor: Tensor of shape (bs, num_systems, 2) and type prec with the state of the signal evolved after the photon counting measurement. If decision_tree=True the shape of this Tensor is (bs, num_systems, 3) and it contains also the whole history of outcomes codified in the last entry.

perform_measurement(controls: Tensor, parameters: Tensor, true_state: Tensor, meas_step: Tensor, rangen: Tensor) → Tuple[Tensor, Tensor, Tensor]

Mixing of the signal with the training state and photon counting on one end of the beam splitter.

Parameters

controls: Tensor: Tensor of shape (bs, 1, 2) and of type prec containing the two angles $\theta$ and $\phi$ characterizing the BS placed before a photon counter.
parameters: Tensor: Tensor of shape (bs, 1, 7) and type prec containing the six real components of the three training states plus the signal class.
true_state: Tensor: Tensor of shape (bs, 1, 2) containing the real components in the phase space of the signal traveling through the apparatus. If decision_tree=True the shape of this Tensor is (bs, 1, 3) and it contains also the whole history of outcomes codified in the last entry.
meas_step: Tensor: Tensor of shape (bs, 1, 1) and type prec. It is the index of the current measurement and starts from zero.
rangen: Generator: Random number generator from the module tensorflow.random.

Return

outcomes: Tensor: Tensor of shape (bs, 1, 1) and type prec containing the number of photons observed in the photon counting measurement.
log_prob: Tensor: Tensor of shape (bs, 1) and type prec containing the logarithm of the probability of getting the observed number of photons.
state: Tensor: Tensor of shape (bs, 1, 2) and type prec containing the state of the signal evolved after the photon counting measurement. If decision_tree=True the shape of this Tensor is (bs, 1, 3) and it contains also the whole history of outcomes codified in the last entry.

class QMLSimulation(particle_filter: ParticleFilter, phys_model: QMLDiscriminator, control_strategy: Callable, simpars: SimulationParameters, loss: int = 0)

Bases: StatefulSimulation

Simulation class for the QML classifier with three states.

Constructor of the QMLSimulation class.

Parameters

particle_filter: ParticleFilter: Particle filter responsible for the update of the Bayesian posterior on the parameters and on the state of the probe.
phys_model: DolinarThree: Abstract description of the QML classifier.
control_strategy: Callable: Callable object (normally a function or a lambda function) that computes the values of the controls for the next measurement from the Tensor input_strategy, which is produced by the method generate_input().
simpars: SimulationParameters: Contains the flags and parameters that regulate the stopping condition of the measurement loop and modify the loss function used in the training.
loss: {0, 1}: In principle the loss of the QML classifier is always the error probability of classifying the state wrongly. However there can be different classification strategies and accordingly different estimators for the error probability. In this class two possible loss functions are implemented. The details are reported in the documentation of the loss_function() method.

generate_input(weights: Tensor, particles: Tensor, state_ensemble: Tensor, meas_step: Tensor, used_resources: Tensor, rangen: Generator) → Tensor

Generates the input to the control strategy (the neural network or the decision tree) starting from the particle filter ensemble.

The values chosen to be inputs of the neural network are similar to those provided in the example of the dolinar module. These are

the average state of the signal after the photon counting measurements, computed from the posterior distribution. These can be 2 ore 6 scalar values according to the architecture of the apparatus,
$(\hat{\alpha}_{0x}, \hat{\alpha}_{0y}, \ \hat{\alpha}_{1x}, \hat{\alpha}_{1y}, \ \hat{\alpha}_{2x}, \hat{\alpha}_{2y})$ , i.e. the average values of the real components of the training states computed from the posterior distribution,
$(\hat{\sigma}_{0x}, \hat{\sigma}_{0y}, \ \hat{\sigma}_{1x}, \hat{\sigma}_{1y}, \ \hat{\sigma}_{2y}, \hat{\sigma}_{2y})$ , i.e. the standard deviation from the mean of the real components of the training states computed from the posterior distribution.

Given $\hat{\sigma}$ one of these deviations, the value passed to the control strategy is actually $-\frac{1}{10} \log \hat{\sigma}$ .
$2 \hat{p}_{0}-1$ , i.e. the posterior probability for the initial state to be s=0, normalized in [-1, +1],
$2 \hat{p}_{1}-1$ , i.e. the posterior probability for the initial state to be s=1, normalized in [-1, +1],
$2 \hat{p}_{2}-1$ , i.e. the posterior probability for the initial state to be s=2, normalized in [-1, +1],
$2 m/M -1$ , i.e. the number of measurements normalized in [-1, +1]. $M$ is the total number measurement and corresponds to the attribute num_steps of DolinarThree, while m is the index of the current photon counting measurement, i.e. meas_step,
$m \bmod 3 - 1$ , this tells whether the current measure is performed by mixing the signal with $| \alpha_0 \rangle$ , $| \alpha_1 \rangle$ , or $| \alpha_2 \rangle$ .

For a serial architecture the number of scalar input is 19, while for a parallel one this number is 23.

Achtung! If decision_tree=True then input_tensor is composed of a single scalar value which encodes the string of outcomes already observed in the measurements.

loss_function(weights: Tensor, particles: Tensor, true_state: Tensor, state_ensemble: Tensor, true_values: Tensor, used_resources: Tensor, meas_step: Tensor)

Returns the estimated error probability for each simulation in the batch. Two possible losses are implemented, and we can select which one to use in the simulation via the parameter loss of the QMLSimulation class constructor. Before defining these losses we need to introduce some notation.

As in generate_input() the posterior Bayesian probabilities of the signal being respectively s=0, 1, 2 are denominated $\hat{p}_0$ , $\hat{p}_1$ , and $\hat{p}_2$ . We introduce the $\delta$ -function, i.e.

(75) $\delta (x, y) = \begin{cases} 1 \quad \text{if} \quad x=y \; , \\ 0 \quad \text{if} \quad x \neq y \; , \end{cases}$

and the guess function $G$ :

(76) $G (\vec{\hat{p}}) = \text{argmax} (\hat{p}_0, \hat{p}_1, \hat{p}_2) \; .$

The first possible loss, corresponding to loss=0, is

(77) $\ell (\vec{\hat{p}}, s) = 1 - \hat{p}_{s} \; ,$

for which the idea is to try to push down the probabilities corresponding to the wrong hypothesis. This loss doesn’t operate on the guess $G (\vec{\hat{p}})$ but directly on the posterior probabilities $\vec{\hat{p}}$ .
The second loss, corresponding to loss=1, is

(78) $\ell (\vec{\hat{p}}, s) = 1 - \delta (G(\vec{\hat{p}}), s) \; .$

This loss is one if an error is made and zero if the guess is right. Averaged on many batches this loss converges to the error probability.

Both losses corresponds to an estimation strategy where the hypothesis with the highest posterior probability is always guessed.

main()

We have trained the quantum Machine Learning classifier for both the parallel and the static architecture, for both losses, and two values of alpha_bound, i.e. $\alpha=0.75$ and $\alpha=1.00$ . We have observed the superiority of the serial architecture and of loss=1 in all the experiments carried out, and accordingly we report in the following only the performances of those simulations. All the estimations have been performed for num_ref=4. The resources are the mean number of photons in the apparatus, as described in the documentation of the count_resources() method.

We studied the performances of the discrimination device in the quantum regime, i.e. with a small number of photons, since for $\alpha \gg 1$ the coherent states are perfectly distinguishable. With $\alpha=0.75$ the signal contains on average 0.5 photons, we should therefore expect relatively high discrimination errors even with optimal strategies. Nevertheless the point of the optimization is to extract every last bit of information from the device, even in a regime where the errors are relatively frequent.

This example is to be taken as less applicative then the others, instead, as a proof of principle of the potentials of the qsensoropt library.

The performances of the neural network and the decision tree are compared to that of the static strategy and to the pretty good measurement (PGM). This last cannot be realized with linear optics and photon counting and assumes a perfect a priori knowledge of the training states $|\alpha_0\rangle$ , $|\alpha_1\rangle$ , and $|\alpha_2\rangle$ . To make a more fair comparison we assumed the PGM consumes 2 num_ref training states where the agnostic Dolinar consumes only num_ref. The extra copies are intended to be used to estimate the training states in order to later perform the corresponding PGM. Still the PGM error probability is not expected to be achievable.

The decision tree computes the next control based on the whole string of outcomes of the previous measurements. Given $\bar{n} = \lfloor \alpha^2 \rceil$ , the outcome $n$ of each measurement is classified into one of the three branches of the tree according to the conditions $n \le \bar{n}-1$ , $n = \bar{n}$ , and $n \ge \bar{n}+1$ . The infinite possibilities for the outcomes (the number of observed photons) gets reduced to only three classes without too much loss of information.

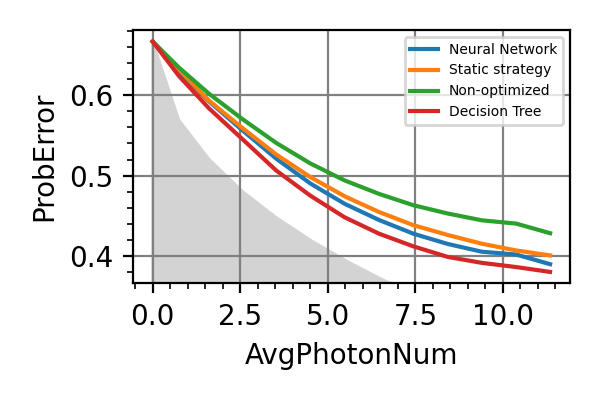
_images/plot_AvgPhotonNum_ProbError.png — Fig. 39 alpha_bound=0.75, loss=1

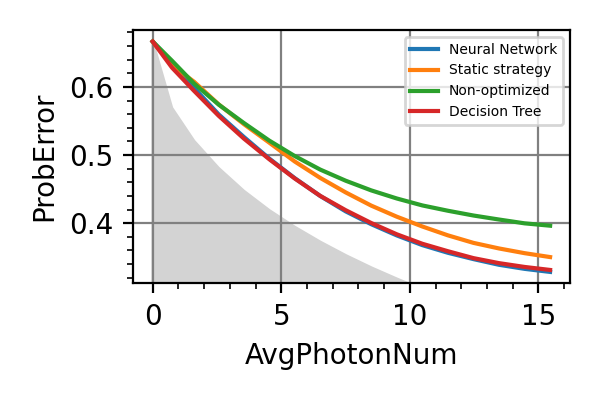
_images/plot_AvgPhotonNum_ProbError1.png — Fig. 40 alpha_bound=1.00, loss=1

The non-optimized strategy refers to a device where the phase imprinted by the beam-splitters are all zero and the reflectivity is chosen, so that the same fraction of the signal reaches each one of the photon counter.

There is an “adaptivity-gap” between the performances of the static controls and the two adaptive strategies (NN and decision tree). This gap starts from zero and grows with the average number of photons. This make sense, since with very few photons we don’t expect the adaptive measurements to be better than the static one, since almost always the measurement outcomes of the photon counters will be zero, which doesn’t give any information about the training states. On the other hand with many photons there is more space for learning. This can be also understood considering the number of possible trajectories of the particle filter ensemble during the estimation, which is one for $\alpha_i = 0$ , and grows with the number of photons. More possible trajectories means having different controls on each one of them in order to improve the precision, which is by definition adaptivity.

In our experiments we observed that the convergence of the NN to the optimal strategy is slow and doesn’t always happen (see the case alpha_bound=0.75 in the figures), while the decision tree is shown to be a superior control for this device. In general, in a problem with many parameters and a relatively small space of possible outcome trajectories, the decision three is superior to the neural network. On the other hand with few parameters and a large space of outcome trajectories (like in the examples on NV centers) the decision three is unapplicable in the form we presented here and the NN is superior.

In the figure on the left the first nodes of the decision tree for alpha_bound=0.75 are shown. The controls from the decision tree have the advantage of being faster to compute with respect to those of the NN, but storing the tree requires more memory. A future work could be to trim the tree by keeping only the paths that correspond to the most probable trajectories (see the figure on the right).

alpha_bound=0.75, decision tree

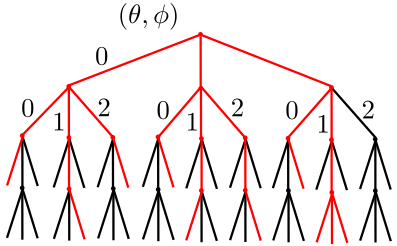
trimmed decision tree

In the following figure five trajectories for the neural network controls $\theta$ and $\phi$ are showed. There is a tendency for the control trajectories to diverge in time (this can be seen well in the plot for $\theta$ ), since having already done some measurements means that the controls can be tailored to the particular instance of the task. This behaviour is trained in the neural network but is hard coded in the decision tree strategy.

_images/plot_MeasStep_Theta.png — Fig. 41 alpha_bound=1.00, loss=1

_images/plot_MeasStep_Phi.png — Fig. 42 alpha_bound=1.00, loss=1

The shaded grey areas in the above plot indicate the performances of the pretty good measurement, computed for multiple copies of the encoded states. This is not the ultimate precision bound regarding this discrimination problems, but it is a reasonable reference value not achievable with linear optics.

The fact the the training is able to find and exploit such small gain from the adaptivity speeks for the efficiency and power of the method.

Notes

For a large number of resources the error probability curves tend to saturate. This is because even with infinite num_ref and therefore perfect knowledge of the training states a single copy of the signal can’t be classified unambiguously.

For the estimation of seven parameter 512 particles in the ensamble are too few. Using 1024 particles improves the performances a bit, but not that much.

We mentioned that loss=1 always outperforms loss=0. This is because with loss=0 we assume that the error probability of the apparatus is the one estimated by the particle filter. In this way, however, the error probability is overeatimated.

In this example we are estimating multiple quantum incompatible parameters, that are the x and p components of the training states and the signal, whose corresponding generators don’t commute.

All the trainings of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB or on a GPU NVIDIA GeForce RTX-4090-24GB, each requiring $\mathcal{O}(1)$ hours.

parse_args()

Arguments

scratch_dir: str: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./qml_classifier/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./qml_classifier/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float64”: Floating point precision of the whole simulation.
batchsize: int = 1024: Batchsize of the simulation.
n: int = 64: Number of neurons per layer in the neural network.
num_particles: int = 512: Number of particles in the ensemble representing the posterior.
num_ref: int = 4: Number of copies of each training state $|\alpha_0\rangle$ , $|\alpha_1\rangle$ , $|\alpha_2\rangle$ .
iterations: int = 32768: Number of training steps.

simulation_qmlclassifier(args, alpha_bound: float = 1.0, learning_rate: float = 0.01, loss: int = 0, arch: str = 'serial')

Simulation of the QML classifier.

Parameters

args:: Arguments passed to the Python script.
alpha_bound: float = 1.0: Size of the hypercube of the admissible values for the real components of the three training states.
learning_rate: float = 1e-2: Initial learning rate for the neural network. The static strategy has a fixed initial learning rate of 1e-1. Both are reduced during the training according to InverseSqrtDecay.
loss: {0, 1}: Type of loss for the training. The two possibilities (loss=0, 1) are discussed in the documentation of the loss_function() method.
arch: {“serial”, “parallel”}: Architecture of device. If it is “serial” then an object QMLDiscriminatorSerial is instantiated for the simulation, if it is “parallel” instead, an object QMLDiscriminatorParallel is instantiated.

Photonic circuit

class FourModesCircuit(batchsize: int, params: List[Parameter], prec: str = 'float64', single_control: bool = False, num_photons: int = 1)

Bases: StatelessPhysicalModel, PhotonicCircuit

Four modes interferometer for the simultaneous estimation of three phases 8.

The interferometer has two balanced quarter as opening and closing elements, which are the generalization of the balanced beam splitter for four modes in input and four modes in output. The three unknown phases are called $\varphi_0, \varphi_1, \varphi_2$ , while the control phases are $c_0, c_1, c_2$ . See also the picture in the documentation of the PhotonicCircuitSimulation class.

8: https://arxiv.org/abs/2209.00671.

Constructor of the FourModesCircuit class.

Parameters

batchsize: int

Number of simultaneous estimations of the phases.

params: List[Parameter]

List of parameters to be estimated, passed to the class constructor. These must be the three unknown phases in the interferometer, with their respective priors.

prec: str = {“float64”, “float32”}

Floating point precision of the simulation.

single_control: bool = False

If this flag is active, then the three control phases in the interferometer, i.e. $c_0, c_1, c_2$ , are all equal to a single control phase $c$ to be optimized, i.e. $c_0=c_1=c_2=c$ .

num_photons: {1, 2, 3, 4}

Mean number of photons in the input state to the interferometer, which is always a collection of coherent states $|\alpha_0 \alpha_1 \alpha_2 \alpha_3\rangle$ . This parameter can take integer values from 1 to 4 (extrema included), and the corresponding input states are

num_photons=1: $\alpha_0=1$ , $\alpha_1=\alpha_2=\alpha_3=0$ ,
num_photons=2: $\alpha_0=\alpha_1=1$ , $\alpha_2=\alpha_3=0$ ,
num_photons=3: $\alpha_0=\alpha_1=\alpha_2=1$ , $\alpha_3=0$ ,
num_photons=4: $\alpha_0=\alpha_1=\alpha_2=\alpha_3=1$ .

An average of one photon at most enters each line of the circuit.

Achtung!: The input states are not Fock states.

count_resources(resources: Tensor, controls: Tensor, true_values: Tensor, meas_step: Tensor) → Tensor: Each execution of the photonic circuit is counted as a consumed resource, and it is called a step.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, meas_step: Tensor, num_systems: int = 1) → Tensor

Returns the log-likelihood of getting a particular outcome for the photon counting measurements on each mode of the interferometer after the closing quarter.

Parameters

outcomes: Tensor: Tensor of shape (bs, num_systems, 4) and type prec containing the number of photons to condition on for each of the four lines.
controls: Tensor: If single_control=False this is a Tensor of shape (bs, num_systems, 3) and of type prec containing the three control phases, while if single_control=True this Tensor has shape (bs, num_systems, 1) and contains the single control phase.
parameters: Tensor: Tensor of shape (bs, num_systems, 3) and type prec containing the ensemble particles for the three unknown phases.
meas_step: Tensor: Tensor of shape (bs, num_systems, 1) and type prec. It is the index of the current execution of the interferometer and starts from zero. We call a single circuit execution, i.e. sending the input and measuring the outcome, a step.
num_systems: int = 1: Number of circuits simulated for each batch element.

Returns

prob: Tensor: Tensor of shape (bs, num_systems) and type prec containing the probability of getting outcomes as a results upon the execution of the photon counting measurement.

perform_measurement(controls: Tensor, parameters: Tensor, meas_step: Tensor, rangen: Generator) → Tuple[Tensor, Tensor]

The input state of the four bosonic modes is fed to the circuit and a photon counting measurement is performed on each output lines after the closing quarter.

Parameters

controls: Tensor: If single_control=False this is a Tensor of shape (bs, 1, 3) and of type prec containing the three control phases, while if single_control=True this Tensor has shape (bs, 1, 1) and contains the single control phase.
parameters: Tensor: Tensor of shape (bs, 1, 3) and type prec containing the true values of the three phases to be estimated $\varphi_0, \varphi_1, \varphi_2$ .
meas_step: Tensor: Tensor of shape (bs, 1, 1) and type prec. It is the index of the current execution of the interferometer and starts from zero. We call a single circuit execution, i.e. sending the input and measuring the outcome, a step.
rangen: Generator: Random number generator from the module tensorflow.random.

Returns

outcomes: Tensor: Tensor of shape (bs, 1, 4) and type prec containing the number of photons observed in the photon counting measurement on each of the four lines.
log_prob: Tensor: Tensor of shape (bs, 1) and type prec containing the logarithm of the probability of getting the observed number of photons.

class PhotonicCircuit(batchsize: int, num_wires: int, prec: str = 'float64')

Bases: CoherentStates

Programmable multimode photonic circuit. Non-linear elements (other than photon counting) can’t be implemented. No homodyne measurement is available.

Constructor of the PhotonicCircuit class.

Parameters

batchsize: int: Number of simultaneous simulations of the circuit.
num_wires: int: Number of bosonic lines in the circuit.
prec: {“float64”, “float32”}: Floating point precision of the simulation.

balanced_beamsplitter_line(state: Tensor, i: int, num_systems: int) → Tensor

Applies a balanced beamsplitter without phase shift between two consecutive bosonic lines.

Parameters

state: Tensor: Tensor of shape (bs, num_systems, 2 num_wires) of type prec containing the real components of the state of the num_wires bosonic modes. The x-components are the entries from 0 to num_wires-1, and the p-components the entries from num_wires to 2 num_wires-1.
i: int: The balanced BS is applied between the i-th and the i+1-th line. The counting starts from zero.
num_systems: int: Size of the second dimension of state. It is the number of circuits simulated for each element of the batch, i.e. for each estimation.

Returns

state: Tensor: Tensor of shape (bs, num_systems, 2 num_wires) of type prec containing the evolved state of the photonic circuit after the application of the beamsplitter.

beamsplitter_line(state: Tensor, theta: Tensor, phi: Tensor, i: int) → Tensor

Controllable beamsplitter between two consecutive lines.

The symbol ? in the shape of a Tensor means that this dimension can have arbitrary size unknown to this method.

Parameters

state: Tensor: Tensor of shape (bs, ?, 2 num_wires) of type prec containing the real components of the state of the num_wires bosonic modes. The x-components are the entries from 0 to num_wires-1, and the p-components the entries from num_wires to 2 num_wires-1.
theta: Tensor: Tensor of shape (bs, ?) and of type prec. It contains the transmission coefficient of the BS. It is indicated with $\theta$ .
phi:: Tensor of shape (bs, ?) and of type prec. It contains the phase applied by the BS. It is indicated with $\phi$ .
i: int: The BS is applied between the i-th and the i+1-th line. The counting starts from zero.

Returns

state: Tensor: Tensor of shape (bs, ?, 2 num_wires) of type prec containing the evolved state of the photonic circuit after the application of the beamsplitter.

phase_shift_line(state: Tensor, phase: Tensor, i: int) → Tensor

Controllable phase shift on the i-th bosonic mode.

The symbol ? in the shape of a Tensor means that this dimension can have arbitrary size unknown to this method.

Parameters

state: Tensor: Tensor of shape (bs, ?, 2 num_wires) of type prec containing the real components of the state of the num_wires bosonic modes. The x-components are the entries from 0 to num_wires-1, and the p-components the entries from num_wires to 2 num_wires-1.
phase: Tensor: Tensor of shape (bs, ?) and type prec containing the phase shift to be applied to the i-th bosonic mode.
i: int: Index of the bosonic mode to be phase shifted. The counting starts from zero.

Returns

state: Tensor: Tensor of shape (bs, ?, 2 num_wires) of type prec containing the evolved state of the photonic circuit.

photon_counting_all(state: Tensor, rangen: Generator) → Tuple[Tensor, Tensor]

Performs the photon counting on each line of the circuit individually.

Parameters

state: Tensor: Tensor of shape (bs, 1, 2 num_wires) of type prec containing the real components of the state of the num_wires bosonic modes. The x-components are the entries from 0 to num_wires-1, and the p-components the entries from num_wires to 2 num_wires-1.
rangen: Generator: Random number generator from the module tensorflow.random.

Returns

outcomes: Tensor: Number of photons observed on each line. It is a Tensor of shape (bs, 1, num_wires) and type prec.
log_prob: Tensor: Log-likelihood of getting the observed outcomes upon the measurement. It is a Tensor of shape (bs, 1) and type prec.

postselect_photon_counting_all(state: Tensor, outcomes: Tensor, num_systems: int = 1) → Tensor

Postselection of the photon counting result on each line of the photonic circuit.

Parameters

state: Tensor: Tensor of shape (bs, num_systems, 2 num_wires) of type prec containing the real components of the state of the num_wires bosonic modes. The x-components are the entries from 0 to num_wires-1, and the p-components the entries from num_wires to 2 num_wires-1.
outcomes: Tensor: Tensor of shape (bs, num_systems, num_wires) and type prec containing the number of photons in each line to condition on.
num_systems: int: Size of the second dimension of state. It is the number of circuits simulated for each element of the batch, i.e. for each estimation.

Returns

log_prob: Tensor: Log-likelihood of getting outcomes as result upon the photon counting measurements. It is a Tensor of shape (bs, num_systems) and type prec.

total_mean_phot(state: Tensor, num_systems: int) → Tensor

Computes the total mean photon number in the photonic circuit.

Given a list of states $\lbrace \alpha_i \rbrace_{i=0}^{n-1}$ for the $n$ bosonic line, this method returns

(79) $N = \sum_{i=0}^{n-1} |\alpha_i|^2 \; .$

Parameters

state: Tensor: Tensor of shape (bs, num_systems, 2 num_wires) of type prec containing the real components of the state of the num_wires bosonic modes. The x-components are the entries from 0 to num_wires-1, and the p-components the entries from num_wires to 2 num_wires-1.
num_systems: int: Size of the second dimension of state. It is the number of circuits simulated for each element of the batch, i.e. for each estimation.

Returns

Tensor:: Mean number of photons present in the entire circuit. It is a Tensor of shape (bs, num_systems) and type prec.

class PhotonicCircuitSimulation(particle_filter: ParticleFilter, phys_model: FourModesCircuit, control_strategy: Callable, simpars: SimulationParameters, random: bool = False)

Bases: StatelessMetrology

Simulation for the FourModesCircuit class.

Achtung! This Simulation class is implemented for unknown phases that are defined as discrete parameters, that is, that can take values only in a finite set. For this reason the task solved here is hypothesis testing.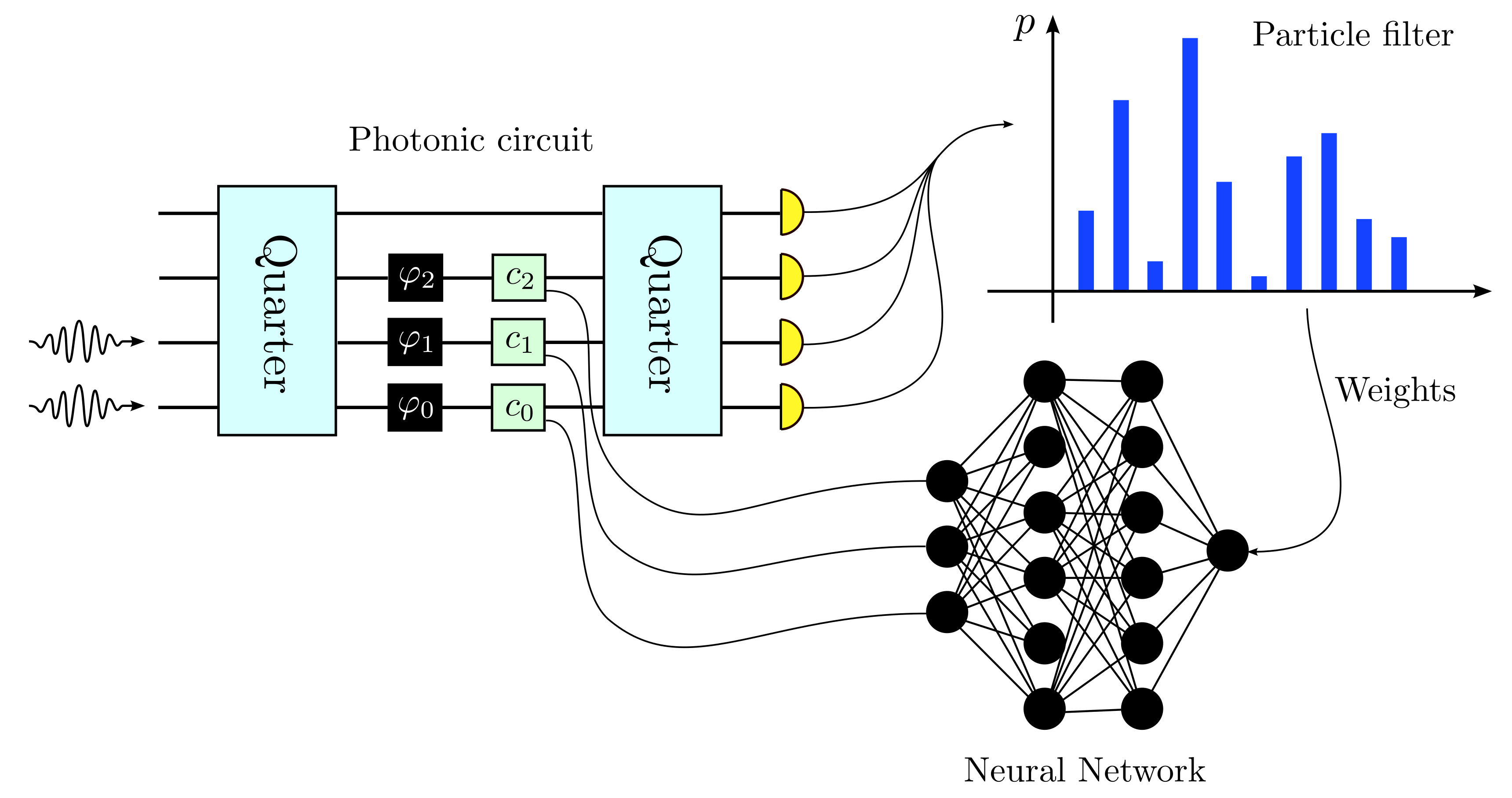

Given the number of possible values $l_0, l_1, l_2$ that each phase can assume, i.e. the length of the values attributes of their respective Parameter objects, the total number of hypothesis to discriminate is $n_h = l_0 l_1 l_2$ . The particle filter contains one and only one particle for each hypothesis along with their corresponding weights $\lbrace w_{j} \rbrace_{j=0}^{n_h-1}$ , that are updated with the Bayes rule after each step.

The posterior distribution on the hypothesis is the input to the control strategy. The loss function loss_function() simply returns the probability of guessing the wrong hypothesis after all the measurements.

Constructor of the PhotonicCircuitSimulation class.

Parameters

particle_filter: ParticleFilter: Particle filter responsible for the update of the Bayesian posterior on the hypothesis.
phys_model: FourModesCircuit: Abstract description of the balanced four mode interferometer.
control_strategy: Callable: Callable object (normally a function or a lambda function) that computes the values of the controls $c_0, c_1, c_2$ for the next step.
simpars: SimulationParameters: Contains the flags and parameters that regulate the stopping condition of the measurement loop and modify the loss function used in the training.
random: bool = False: If this flag is True a column of random numbers extracted uniformly in $[0, 2 \pi]$ is appended to the input_tensor generated by generate_input() for each control in the circuit. The number of controls can be either three or one according to the flag single_control of phys_model.

generate_input(weights: Tensor, particles: Tensor, meas_step: Tensor, used_resources: Tensor, rangen: Generator) → Tensor

Generates the input_tensor passed to control_strategy, on the basis which the next controls are predicted.

The input_tensor is composed on the following columns:

weights, i.e. the posterior distribution on the possible values of the phases. These are $n_h$ columns,
meas_step normalized in [-1, +1],
used_resources normalized in [-1, +1].
one or three columns of random numbers uniformly extracted in $[0, 2 \pi)$ . This is present only if random=True.

The shape of the returned input is (bs, input_size), with input_size being $n_h+2$ if random=False or $n_h+5$ if random=True and single_control=False.

loss_function(weights: Tensor, particles: Tensor, true_values: Tensor, used_resources: Tensor, meas_step: Tensor) → Tensor

Loss function for the hypothesis testing in the four arms interferometer.

On each estimation in the batch the loss is zero if the correct phases are guessed correctly and one if they are guessed wrongly. In symbols, given the delta function

(80) $\delta (x, y) = \begin{cases} 1 \quad \text{if} \quad x=y \; , \\ 0 \quad \text{if} \quad x \neq y \; , \end{cases}$

the guess based on the Bayesian posterior is

(81) $G \left( \lbrace w_j \rbrace_{j=0}^{n_h} \right) = \text{argmax} (w_0, w_1, \dots w_{n_h-1}) \; ,$

and calling $s$ the index of the correct hypothesis for the phases values the loss can be expressed as

(82) $\ell \left( \lbrace w_j \rbrace_{j=0}^{n_h} , s \right) = 1 - \delta (G, s) \; ,$

which, averaged on the batch is the error probability.

main()

In the following we report the evaluated error probability in the correct identification of three phases in a four arms interferometer with various input states. Each phase can assume the two values $\varphi_i \in \lbrace 0, 1 \rbrace$ . The three phases $c_0, c_1, c_2$ can be controlled, see the picture in the documentation of the PhotonicCircuitSimulation class, and the performances of three control strategies have been compared for the same input states.

With this circuit we are testing in parallel for each slot whether a phase shift is there or not. This phase shift could be due to the presence of a certain object, a chemical species, or it could be a piece of codified information.

The following plots represent the probability of guessing the unknown phases wrong as a function of the mean number of photons consumed in the estimation and of the number of measurements, for the adaptive, the static, and the random strategies.

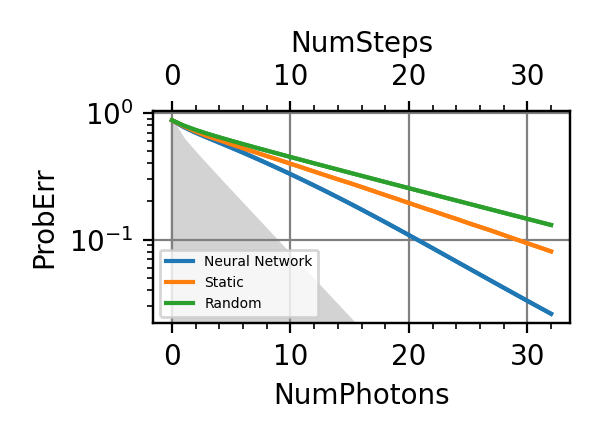
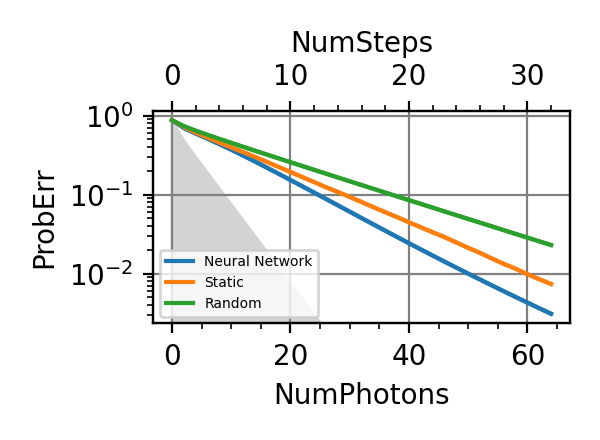
Fig. 43 num_photons=1	Fig. 44 num_photons=2
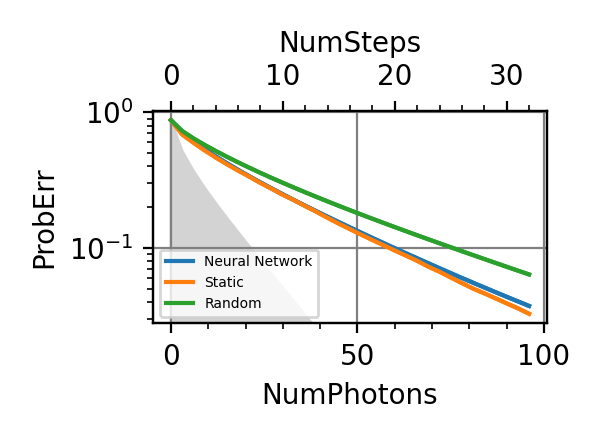
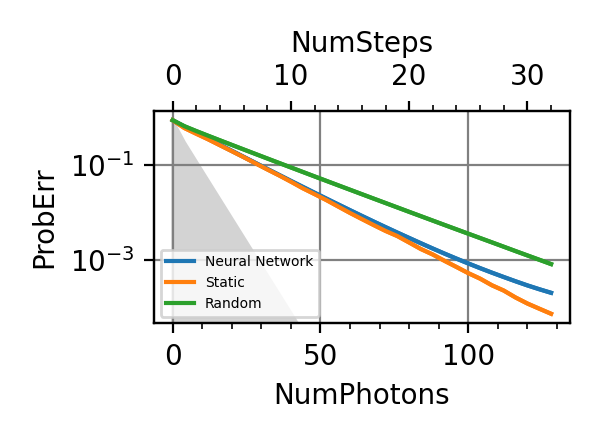
Fig. 45 num_photons=3	Fig. 46 num_photons=4

Only for num_photons=1, 2 the adaptive strategy has been proven to give some advantage with respect to the static one. The state with three photons doesn’t perform well in comparison to all the other inputs. The best input in terms of the consumed number of photons to reach a certain probability error is the state with a single photon on average. It is possible that in terms of the damage caused to the sample or the energy used (which are both proportional to the total number of photons) performing many measures each with a vanishingly small photon number is optimal. This hypothesis should be verified with more simulations in the range num_photons<1. If it that is the case, then minimizing the energy or the damage would mean stretching the total measurement time, which could also be unfeasible beyond a certain amount. For a fixed number of measurements, therefore for a fixed estimation time, the states with many photons seem to perform better then those with less photons (num_photons=3 being an exception). The fact that for different resources either the states with many of with few photons are optimal underlines the importance of clearly identifying the resource when discussing metrology. Other simulations should be performed for the input states $|2000\rangle$ , $|3000\rangle$ and $|4000\rangle$ to asses their usefulness.

Notes

Known bugs: the training on the GPU freezes if the number of input photons is too large. This is probably due to a bug in the implementation of the function random.poisson. A preliminary work-around has shown that reimplementing the extraction from a Poissonian distribution with random.categorical would solve the problem.

All the training of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

parse_args()

Arguments

scratch_dir: str: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./photonic_circuit/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./photonic_circuit/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float64”: Floating point precision of the whole simulation.
batchsize: int = 4096: Batchsize of the simulation.
n: int = 64: Number of neurons per layer in the neural network.
num_steps: int = 32: Number of uses of the interferometer, i.e. number of measurements in the hypothesis testing.
iterations: int = 32768: Number of training steps.

photonic_circuit_estimation(args, learning_rate: float = 0.01, gradient_accumulation: int = 1, cumulative_loss: bool = True, phase_values: Tuple = (0, 1), single_control: bool = False, num_photons: int = 1)

Simultaneous estimation of three phases in the four arms interferometer as describe by the FourModesCircuit class.

Each call to this function will perform the hypothesis testing on the values of the three phases for three strategies, i.e. the adaptive one implemented with a NN, the static, and the random strategies.

Parameters

args:: Arguments passed to the Python script.
learning_rate: float = 1e-2: Initial learning rate for the neural network. The static strategy has a fixed initial learning rate of 1e-1. Both are reduced during the training according to InverseSqrtDecay.
gradient_accumulation: int = 1: Flag of the train() function.
cumulative_loss: bool = True: Flag cumulative_loss. Set for all the simulations.
phase_values: Tuple = (0, 1): Contains the possible discrete values that each phase $\varphi_i$ can assume independently.
single_controls: bool = False: If the function is called with single_control=True, then it will evaluate the performances of the adaptive, random, and static strategies in the scenario where the three controllable phases are all equal, i.e. $c_0=c_1=c_2=c$ , and there is therefore only a single scalar control $c$ . This flag is used in the initialization of the FourModesCircuit object.
num_photons: int = 1: Mean number of photons in the input state of the interferometer for each measurement step. This values is used in the initialization of the FourModesCircuit object.

Linear Multiclassifier

class ClassifierSimulation(particle_filter: ParticleFilter, phys_model: LinearMulticlassifier, control_strategy: Callable, simpars: SimulationParameters, random: bool = False)

Bases: StatelessSimulation

Simulation class associated to the LinearMulticlassifier physical model.

Attributes

bs: int: Batchsize of the simulation.
phys_model: LinearMulticlassifier: Parameter phys_model passed to the class constructor.
control_strategy: Callable: Parameter control_strategy passed to the class constructor.
pf: ParticleFilter: Parameter particle_filter passed to the class constructor.
input_size: int: This attribute depends on the flag random. If random=False then input_size=1 while if random=True then input_size=2 phys_model.num_wires^2.
input_name: List[str]: If random=False then this list contains only the string “MeasStepOverMaxStep”, while if random=True then it contains the name of all the BS network parameters, i.e. $a_{ij}$ and $b_{ij}$ for $i=0, 1, \cdots, m$ and $j=0, 1, \cdots, m$
simpars: SimulationParameters: Parameter simpars passed to the class constructor.
num_layers: int: Number of BS layers in the signal estimation. It is the num_steps attribute of simpars. It is indicated also with $N$ in the formulas.
random: bool = False: Flag random passed to the class constructor.

Constructor of the ClassifierSimulation class.

Parameters

particle_filter: ParticleFilter: Particle filter responsible for the update of the Bayesian posterior on the hypothesis.
phys_model: LinearMulticlassifier: Abstract description of the linear multiclassifier.
control_strategy: Callable: Callable object (normally a function or a lambda function) that computes the values of the controls for the next measurement from the Tensor input_strategy. If random=False then input_strategy contains only the (renormalized) index of the current layer and the control_strategy should return the corresponding BS parameters to be optimized. If on the other hand random=True input_strategy contains a randomly extracted parametrization of a BS network, that control_strategy can immediately return.
simpars: SimulationParameters: Contains the flags and parameters that regulate the stopping condition of the measurement loop and modify the loss function used in the training.
random: bool = False: If this flag is True the 2 phys_model.num_wires^2 randomized controls for the BS network are added to the output of the generate_input() method.

generate_input(weights: Tensor, particles: Tensor, meas_step: Tensor, used_resources: Tensor, rangen) → Tensor

Builds the input_strategy tensor.

If random=False this method returns $n/N$ , where $n$ is meas_step, i.e. the index of the current layer and $N$ is the total number of layers, i.e. the attribute num_layers. This is a Tensor of shape (bs, 1) and type prec
If, on the other hand, random=True this method returns $2 (m+1)^2$ randomly extracted angles in $(0, 2 \pi)$ , which identify a BS network. This is a Tensor of shape (bs, 2 phys_model.num_wires^2) and type prec.

loss_function(weights: Tensor, particles: Tensor, true_values: Tensor, used_resources: Tensor, meas_step: Tensor) → Tensor

After all the measurements have been performed the particle filter contains a discrete distribution of posterior probabilities for the signal classes, i.e. $\mathfrak{p} = \lbrace \hat{p}_i \rbrace_{i=1}^{m-1}$ . The guess for the signal class is defined by the function

(83) $G(\mathfrak{p}) = \text{argmax} (\hat{p}_0, \hat{p}_1, \cdots, \hat{p}_{m-1}) \; ,$

and the loss is

(84) $\ell (\mathfrak{p}, s) = 1 - \delta (G(\mathfrak{p}), s) \; ,$

with

(85) $\delta (x, y) = \begin{cases} 1 \quad \text{if} \quad x=y \; , \\ 0 \quad \text{if} \quad x \neq y \; , \end{cases}$

Averaged on many batch $\ell (\mathfrak{p}, s)$ approximates the error probability.

class LinearMulticlassifier(batchsize: int, list_alphas: Tuple[complex], prec: str = 'float64')

Bases: StatelessPhysicalModel, PhotonicCircuit

Model for a network of beam splitters (BS) and phase shifts that receives as input the signal $|\alpha_s\rangle$ to be classified, with $s \in \lbrace 0, 1, \dots, m-1 \rbrace$ being the classes. The number $m$ is the attribute num_hypothesis and the length of the tuple list_alphas passed to the constructor.

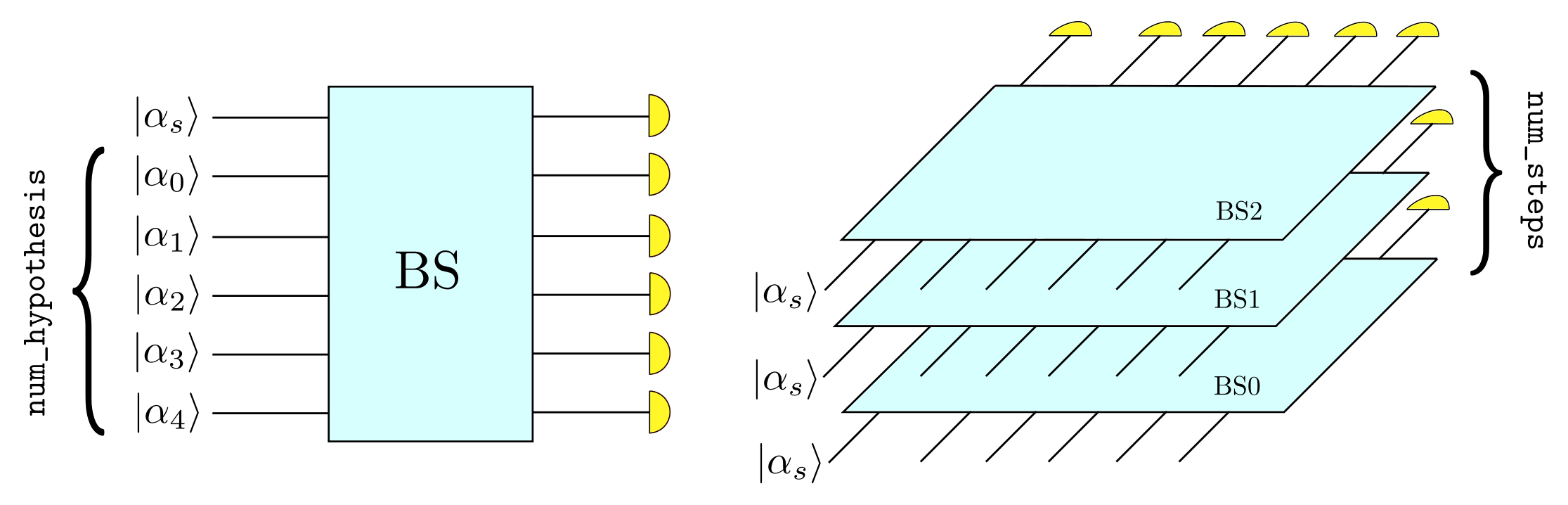
The other inputs of the network are in order $|\alpha_0\rangle$ , $|\alpha_1\rangle$ , $|\alpha_2\rangle$ , …, $|\alpha_{m-1}\rangle$ , that is, the reference states corresponding to the possible hypothesis (classes), which, at difference with the example of the dolinar_three are fixed for each execution of the task. It follows that the network has $m+1$ wires. The output of the network is measured with individual photon counters on each wire.

The signal $|\alpha_s\rangle$ will be classified according to the photon counters outcomes. If more than one signal state is available multiple BS networks can be stacked on one another and the classification will be based on the measurements on all the layers. Each layer can have a different network BS0, BS1, …

Attributes

bs: int: Batchsize of the simulation.
list_alphas: Tuple[complex]: List of reference states. It is a parameter passed to the class constructor.
num_hypothesis: int: Number of classes or hypothesis. It is the length of the tuple list_alphas. It is also indicated with the symbol $m$ .
num_wires: int: Number of wires in the network. It is num_hypothesis+1, i.e. $m+1$ .
controls: List[Control]: Real parameters identifying the BS network.
params: List[Parameter]: Contains the description of the unknown to be estimated, i.e. the discrete parameter Signal that takes values in the set $\lbrace 0, 1, \cdots, m-1 \rbrace$ . The initial value randomization must be disabled in this application, i.e. the flag randomize of the Parameter constructor must be set to False. In this way initializing $m$ particle in the ParticleFilter will produce particles with values $0, 1, \cdots, m-1$ in this order and without repetitions.
controls_size: int: Number of real parameters of the BS network, i.e. $2 (m+1)^2$ .
d: int = 1: Number of unknown parameters to estimate, i.e. one, the signals class.
outcomes_size: int: Number of scalar outcomes for each layer of networks, i.e. the number of wires $m+1$ .
prec: str: Floating point precision of the controls, outcomes, and parameters.

Constructor of the LinearMulticlassifier class.

Parameters

batchsize: int: Number of simultaneous estimations.
list_alphas: Tuple[complex]: Tuple of complex numbers $(\alpha_0, \alpha_1, \dots, \alpha_{m-1})$ that represent the reference states.
prec: = {“float64”, “float32”}: Floating point precision of the controls, outcomes, and parameters.

count_resources(resources: Tensor, controls: Tensor, true_values: Tensor, meas_step: Tensor) → Tensor: The execution of each BS layer is counted as a consumed resource.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, meas_step: Tensor, num_systems: int = 1) → Tensor

Returns the probability of getting a certain number of photons after the application of the BS network to the input state $|\alpha_s\rangle \otimes |\alpha_0\rangle, \otimes |\alpha_1\rangle \otimes \cdots \otimes |\alpha_{m-1}\rangle$ .

Parameters

outcomes: Tensor: Tensor of shape (bs, num_systems, num_wires) and type prec containing the number of photons measured on each wire of the system after the application of the network.
controls: Tensor: Tensor of shape (bs, num_systems, 2 num_wires^2) and type prec that parametrizes the BS network.
parameters: Tensor: Tensor of shape (bs, num_systems, 1) and type prec that contains the class s of the signal $|\alpha_s\rangle$ for each particle in the particle filter ensemble.
meas_step: Tensor: Tensor of shape (bs, num_systems, 1) and type int32 that contains the index of the current BS layer. It starts from zero.
num_systems: int = 1: Number of BS networks processed per batch.

Returns

prob: Tensor: Tensor of shape (bs, num_systems) of type prec containing the probabilities of getting the number of photons outcomes after the BS network defined by controls has been applied on the signal defined by parameters.

perform_measurement(controls: Tensor, parameters: Tensor, meas_step: Tensor, rangen: Generator) → Tuple[Tensor, Tensor]

Application of the BS network to the input state $|\alpha_s\rangle \otimes |\alpha_0\rangle \otimes |\alpha_1\rangle \otimes \cdots \otimes |\alpha_{m-1}\rangle$ and subsequent photon counting measurements on all the wires.

Parameters

controls: Tensor: Tensor of shape (bs, 1, 2 num_wires^2) and type prec that parametrizes the BS network.
parameters: Tensor: Tensor of shape (bs, 1, 1) and type prec that contains the class s of the signal $|\alpha_s\rangle$ for each element of the batch.
meas_step: Tensor: Tensor of shape (bs, 1, 1) and type int32 that contains the index of the current BS layer. It starts from zero.
rangen: Generator: Random number generator from the module tensorflow.random.

Returns

outcomes: Tensor: Tensor of shape (bs, 1, num_wires) and type prec containing the number of photons measured on each wire of the system after the application of the BS network.
log_prob: Tensor: Tensor of shape (bs, 1) and type prec containing the logarithm of the probability of getting the observed number of photons (the likelihood).

bs_network_classify(args, batchsize: int, list_alphas: Tuple[complex], learning_rate: float = 0.1)

Runs the training of the linear multiclassifier for the list of reference states list_alphas. Compares the performances of the trained BS networks with that of randomly extracted networks.

Parameters

args:: Arguments passed to the Python script.
batchsize: int: Number of simultaneous classifications.
list_alphas: Tuple[complex]: Tuple of complex numbers $(\alpha_0, \alpha_1, \dots, \alpha_{m-1})$ that represent the reference states.
learning_rate: float = 1e-1: Initial learning rate for the training of the BS network. The learning rate is reduced during the training according to InverseSqrtDecay.

Notes

Known bugs: the training on the GPU freezes if the number of photons in the apparatus is too large. This is probably due to a bug in the implementation of the function random.poisson. A preliminary work-around has shown that reimplementing the extraction from a Poissonian distribution with random.categorical would solve the problem.

At difference with other examples we haven’t used a neural network here, and therefore we don’t have adaptivity.

All the training of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

main()

The linear multiclassifier has been trained and tested for some symmetric configurations of the $\alpha_i$ . In particular the roots of the unit for $m=3, 5, 7, 9$ have been chosen. For a symmetric configuration of states the pretty good measurement (PGM) is optimal, but it can’t be achieved with linear optics. The optimality of the PGM means that a single layer BS network can’t achieve the performances of the PGM, however this raises the interesting question of how many layers (and copies of the signal $|\alpha_s\rangle$ ) are necessary to match or surpass the error probability of the PGM. Beside that, the performances of the trained BS networks are also compared to that of randomly extracted networks.

The following plots represent the error probability in the classification of the signal versus the number of layers of the linear multiclassifier (a single “resources” is the execution of a layer).

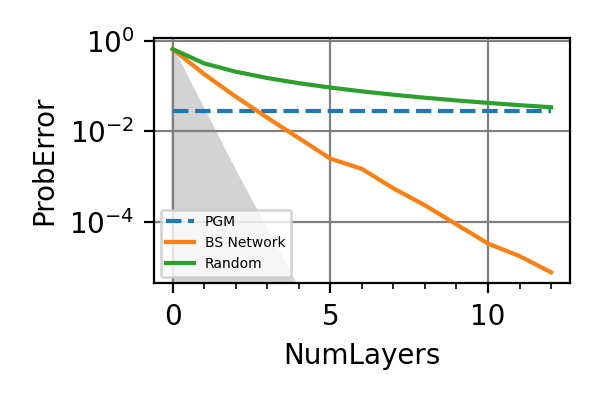
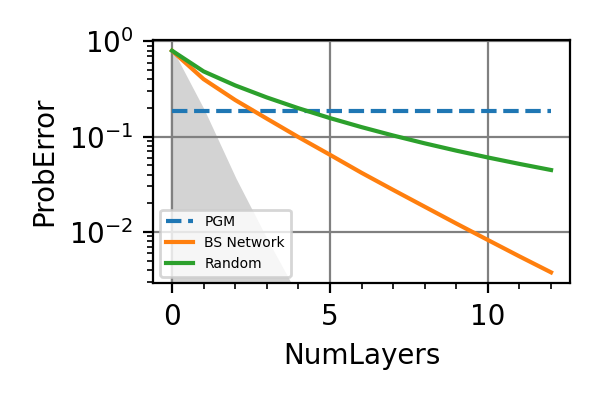
Fig. 47 m=3	Fig. 48 m=5
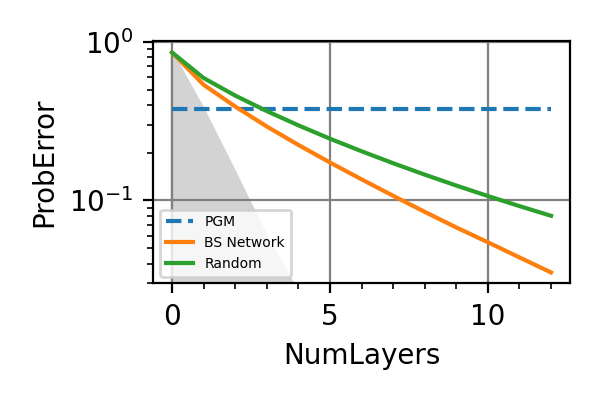
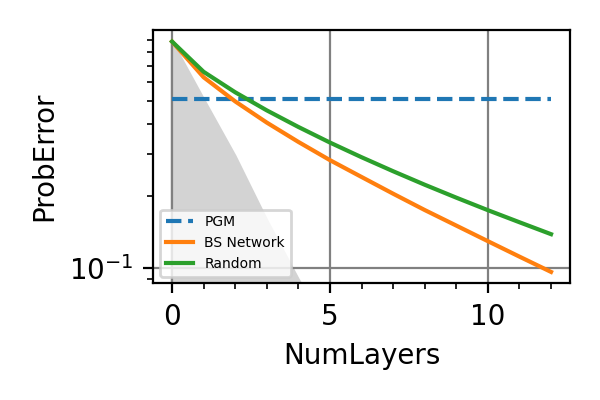
Fig. 49 m=7	Fig. 50 m=9

The shaded grey areas in the above plot indicate the error probability of the PGM for many copies of the signal.

Three copies of the signal are always sufficient in these examples to match the PGM error probability. An interesting observation is that the advantage over the random strategy that the trained network has, decreases as the number of hypothesis grows. For $m \rightarrow \infty$ we expect to have no gain. An adaptive strategy may be able to restore the gap with the untrained BS networks.

This example has been suggested to us by L. Bagnasacco.

Notes

In this example we are estimating two quantum incompatible parameters, that are the x and p components of the signal state, whose corresponding generators don’t commute.

All the training of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

parse_args()

Arguments

scratch_dir: str: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./linear_multiclassifier/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./linear_multiclassifier/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float64”: Floating point precision of the whole simulation.
batchsize: int = 8192: Batchsize of the simulation.
num_layers: int = 12: Maximum number of layers of BS network.
iterations: int = 4096: Number of training steps.

roots_of_unity(n: int)

Returns the the n-th roots of the unit.

Parameters

n: int: Index of the root.

Returns

roots: Tuple: Tuple of shape (n, ) containing the unit roots.

Optical Cavity

class CavityParameters(delta_time: float, kappa: float, chi: float, num_photons: float, init_displacement: float, omega: float)

Bases: object

Physical parameters of the optical cavity.

chi: float: Squeezing parameter of the non-linear crystal inside the cavity.

delta_time: float: Time between two consecutive homodyne detections.

init_displacement: float: Magnitude of the initial displacement of the cavity state in the phase space along the direction (1, 1).

kappa: float: Fraction of the signal extracted at each homodyne measurement per second.

num_photons: float: Thermal noise in the initial state of the cavity, i.e. number of photons in the thermal state.

omega: float: Detuning between the cavity and the driving laser frequencies. It is the parameter to be sensed.

class OpticalCavity(batchsize: int, params: List[Parameter], cav_parameters: CavityParameters, prec: str = 'float64')

Bases: StatefulPhysicalModel

Abstract model for an optical cavity with a single mode, that can be measured via homodyne detection.

This model is taken from the paper of Fallani et al. 9.

9: A. Fallani, M. A. C. Rossi, D. Tamascelli, and M. G. Genoni, PRX Quantum 3, 020310 (2022).

Constructor of the OpticalCavity class.

Parameters

batchsize: int: Number of simultaneous estimations of the detuning frequency.
params: List[Parameter]: List of unknown parameters to be estimated in the optical cavity experiment. It should contain the parameter Omega, i.e. the detuning frequency, with a single possible admissible value, that is the point at which the sensing is performed.
cav_parameters: CavityParameters: Contains the values of the physical parameters of the cavity.
prec: {“float64”, “float32”}: Floating point precision of the estimation.

count_resources(resources: Tensor, controls: Tensor, true_values: Tensor, meas_step: Tensor) → Tensor: The consumed resource is the total evolution time. We consider the measurements instantaneous and spaced of $\Delta t$ . Therefore $n$ measurements consume a total amount of time $n \Delta t$ .

initialize_state(parameters: Tensor, num_systems: int) → Tensor

Initialization of the cavity state.

The initial state of the cavity is Gaussian and so are all the operations performed on it, therefore it remains Gaussian. Accordingly the state can be described with the covariance matrix $\sigma$ and the displacement vector $\vec{r}$ . This method returns the initial state of the cavity described by

(86) $\vec{r} = \frac{1}{\sqrt{2}}(r_0, r_0) \quad \text{and} \quad \sigma = (2 n_{th} + 1) \mathbb{I} \; ,$

where $r_0$ is init_displacement and $n_{th}$ is num_photons.

Parameters

parameters: Tensor: Tensor of shape (bs, num_systems, 1) containing the values of Omega. It is not used for producing the initial state.
num_systems: int: Size of the second dimension of parameters. It is the number of cavity states instantiated for each batch element, i.e. for each estimation.

Returns

initial_state:: Tensor of shape (bs, num_systems, 6) containing tha flattened and concatenated displacement vector $\vec{r}_0$ and covariance matrix $\sigma$ of cavity initial Gaussian state.

model(outcomes: Tensor, controls: Tensor, parameters: Tensor, state: Tensor, meas_step: Tensor, num_systems: int = 1) → Tuple[Tensor, Tensor]

Returns the probability for the homodyne detection on the cavity field to give a certain outcome.

Parameters

outcomes: Tensor: Tensor of shape (bs, num_systems, 1) and type prec containing the outcomes of the homodyne measurement to postselect on.
controls: Tensor: Tensor of shape (bs, num_systems, 1) and type prec containing the feedback frequency $\omega_f$ of the driving laser.
parameters: Tensor: Tensor of shape (bs, num_systems, 1) and type prec containing the detuning frequency $\omega$ of the cavity at which the point estimation is performed.
state: Tensor: Tensor of shape (bs, num_systems, 6) and type prec containing the displacement vector and the covariance matrix of the Gaussian state of the cavity.
meas_step: Tensor: Tensor of shape (bs, num_systems, 1) and type prec. It is the index of the current homodyne measurement and it starts from zero.
num_systems: int = 1: Number of optical cavities simulated per batch, i.e per estimation.

Returns

prob:: Probability for the homodyne detection to return outcomes after the state has been evolved for a time $\Delta t$ . It is a Tensor of shape (bs, num_systems) and type prec.
state:: State of the cavity conditioned on the observation of outcomes. It is a Tensor of shape (bs, num_systems, 6) and of type prec.

perform_measurement(controls: Tensor, parameters: Tensor, true_state: Tensor, meas_step: Tensor, rangen: Generator) → Tuple[Tensor, Tensor, Tensor]

Evolves the cavity for a time $\Delta t$ , then performs a homodyne detection on the fraction of the cavity field that leaks out through the partially reflective mirror.

For each measurement the state of the cavity is virtually splitted on a beam-splitter with transmission coefficient $\kappa \Delta t$ , where $\Delta t$ is delta_time and $\kappa$ is kappa. The reflected part stays in the cavity, while the transmitted part is measured through homodyne detection, which causes a backreaction on the light remaining in the cavity (because of the squeezing of the cavity mode).

Parameters

controls: Tensor: Tensor of shape (bs, 1, 1) and type prec containing the feedback frequency $\omega_f$ of the driving laser.
parameters: Tensor: Tensor of shape (bs, 1, 1) and type prec containing the detuning frequency $\omega$ of the cavity, at which the point estimation must be performed.
true_state: Tensor: Tensor of shape (bs, 1, 6) and type prec containing the displacement vector and the covariance matrix of the Gaussian state of the cavity at the moment of the call of this method.
meas_step: Tensor: Tensor of shape (bs, 1, 1) and type prec. It is the index of the current homodyne measurement and it starts from zero.
rangen: Generator: Random number generator from the module tensorflow.random.

Returns

u: Tensor: Tensor of shape (bs, 1, 1) and type prec that contains the outcome of the homodyne detection on the cavity mode.
log_prob: Tensor: Log-likelihood of having observed the outcome u. It is a Tensor of shape (bs, 1) and type prec.
true_state: Tensor: Evolved state of the cavity after the application of the backreaction. It is a Tensor of shape (bs, 1, 6) and type prec.

unitary_evolution(state: Tensor, parameters, controls, num_systems: int = 1) → Tensor

Returns the state of the cavity after the unitary evolution of time duration delta_time, with external driving.

The evolution of the Gaussian state of the cavity due to the detuning and the non-linear crystal is described by the following differential equations for $\vec{r}(t)$ and $\sigma(t)$ :

(87) $\frac{d \vec{r}(t)}{dt} = A \vec{r} (t) \; ,$

(88) $\frac{d \sigma(t)}{dt} = A \sigma(t) + \sigma(t) A^T \; ,$

with

(89) $A = \begin{pmatrix} -\chi & \omega + \omega_f \\ -(\omega+\omega_f) & \chi \end{pmatrix} \; ,$

where $\chi$ is chi, i.e. the squeezing parameter, and $\omega$ is omega, i.e. the detuning. $\omega_f$ is the parameter controls and is determined by the external driving.

These differential equations can be solved exactly:

(90) $\vec{r} (t+\Delta t) = e^{A \Delta t} \vec{r} (t) \; ,$

(91) $\sigma (t+\Delta t) = e^{A \Delta t} \sigma (t) e^{A^T \Delta t} \; ,$

where $\Delta t$ is delta_time, i.e. the evolution time.

Parameters

state: Tensor: Tensor of shape (bs, num_systems, 6) containing the evolved state of the cavity before the evolution. It is the concatenation of the flattened versions of the moments $\vec{r}(t)$ and the covariance matrix $\sigma (t)$ .
parameters: Tensor: Tensor of shape (bs, 1, 1) containing the value of the detuning frequency $\omega$ .
num_systems: int = 1: Number of optical cavities simulated per batch element, i.e. per estimation.

Returns

state: Tensor: Tensor of shape (bs, num_systems, 6) containing the evolved state of the cavity. It is the Tensor obtained by concatenating the flattened versions of $\vec{r}(t+\Delta t)$ and $\sigma(t+\Delta t)$ .

Notes

In order to compute the exponential of the traceless matrix $A \Delta t$ there is an handy formula:

(92) $e^{A \Delta t} = \cos (\Delta t \sqrt{|A|}) \mathbb{I} + \frac{\sin (\Delta t \sqrt{|A|})}{\sqrt{|A|}} A \; ,$

where $|A|$ is the determinant of $A$ . This formula works for both $|A|>0$ and $|A|<0$ .

main()

We trained both the adaptive and the static strategies for controlling the feedback frequency and we found no advantage in using a neural network for all the values of $\chi$ that we have explored. In the following we report on the left the Fisher information per unit of time, i.e. $F_t = F/T$ as a function of the evolution time $T$ for the optimal adaptive strategies, and on the right a plot of the squeezing parameter

(93) $\xi_{dB} = -20 \log \frac{\sigma_x}{\sigma_p} \; ,$

computed as function of time.

_images/plot_EvolutionTime_F_t.png — Fig. 51 Fisher/Time

_images/plot_EvolutionTime_Xi_dB.png — Fig. 52 Squeezing parameter

The point of the optimal strategies is to create squeezing on the x-axis (the one measured by the homodyne detection) and position the state on the p axis as far as possible from the origin, so that the rotation sensitivity is maximized.

In the following plots we report the mean value of the displacement in the phase space for the cavity state, always as a function of time.

At the very beginning the states spread on the x-axis due to the relative high initial thermal noise and the homodyne measurement backreaction, but at the end the controls have managed to give the states a p-components and to reduce the displacement along the x-axis.

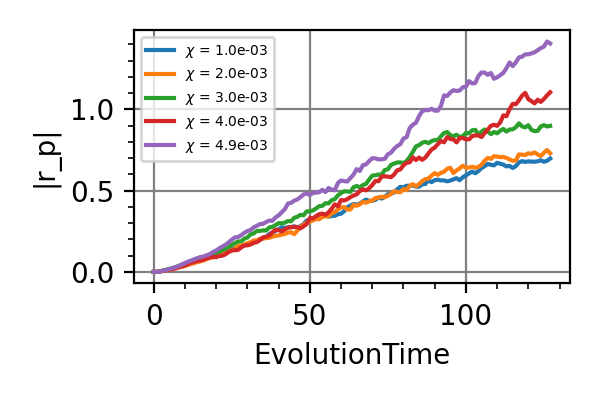
_images/plot_EvolutionTime_%7Cr_p%7C.png — Fig. 53 Mean of $|r_p|$ .

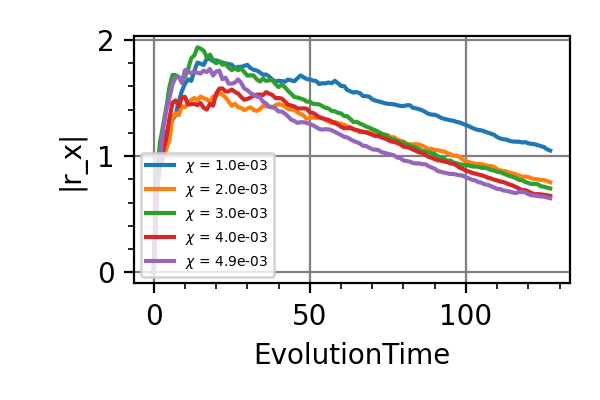
_images/plot_EvolutionTime_%7Cr_x%7C.png — Fig. 54 Mean of $|r_x|$ .

Notes

If instead of fixing $\omega$ we had a interval of possible values for the parameter, i.e. by setting the flag interval of the function optimize_optical_cavity(), the neural network would be useful to modulate the optimal strategy as a function of $\omega$ .

All the training of this module have been done on a GPU NVIDIA Tesla V100-SXM2-32GB, each requiring $\mathcal{O}(1)$ hours.

optimize_optical_cavity(args, chi: float, interval: bool = False)

Training of the optimal controls for the feedback frequency of the driving laser in the cavity in order to minimize the Cramér-Rao (CR) bound. This function evaluates the performances of a trained neural network, of a static (open-loop) strategy, and of the random controls.

While the squeezing parameters $\chi$ is variable and passed to the call of the function through the parameter chi, all the other attributes of CavityParameters are fixed to $\Delta t = 1, \, \kappa = 10^{-2}, \, n_{th} = 5, \, r_0 = 0, \, \omega = 10^{-3}$ .

With approximately 1% of the cavity field measured by the homodyne detection at every step we are in the regime of continuous measurements.

Parameters

args:: Arguments passed to the Python script.
chi: float: Squeezing parameter of the non-linear crystal in the cavity.
interval: bool = False: If this flag is True, the minimization of the CR bound is done in the range of detuning frequency $(\omega, 10 \omega)$ .

parse_args()

Arguments

scratch_dir: str: Directory in which the intermediate models should be saved alongside the loss history.
trained_models_dir: str = “./optical_cavity/trained_models”: Directory in which the finalized trained model should be saved.
data_dir: str = “./optical_cavity/data”: Directory containing the csv files produced by the performance_evaluation() and the store_input_control() functions.
prec: str = “float64”: Floating point precision of the whole simulation.
n: int = 64: Number of neurons per layer in the neural network.
batchsize: int = 16: Batchsize of the simulation.
evolution_time: int = 128: Total evolution time of the cavity.
learning_rate: float = 1e-2: Initial learning rate for the neural network.
iterations: int = 1024: Number of training steps.